1986年に発表された『誤差逆伝播法』によって第2次AIブームが起きた際、このパターン認識技術が自動運転を可能にさせるに至るとの思いをはせた人達にとっては、現実との極端なギャップ感(夢物語の実現が遠い将来に起きうる)を抱いたと思う。
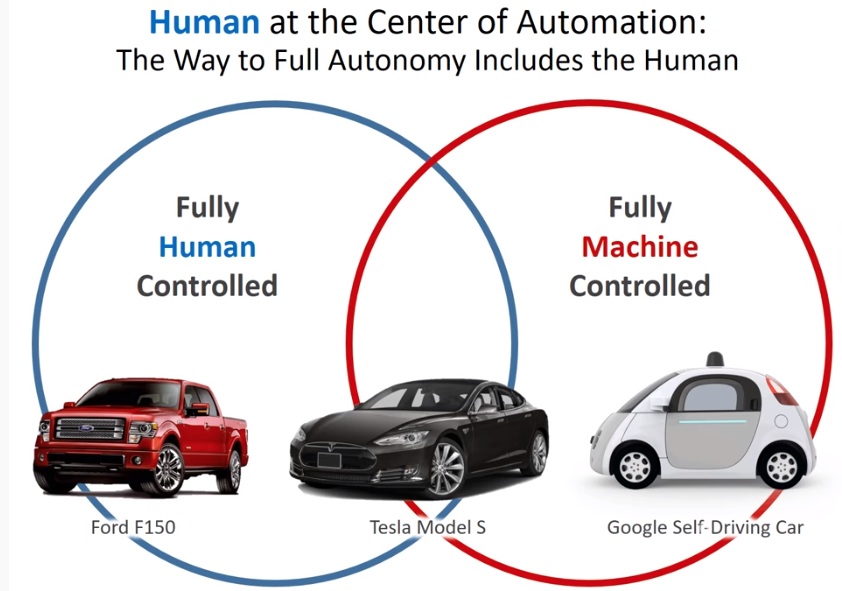
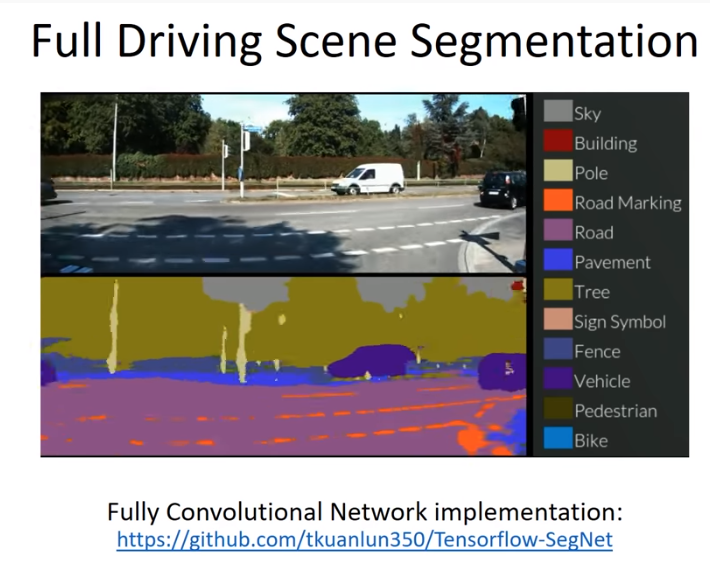
今日、テスラやGoogleで代表される公道での自動運転実験やその事故例も知っているが、 AI音声アシスタントによる日常生活への利便さは広く実感させられるに至っている。
1986年当時(誤差逆伝播法の発見)では夢物語で片づけられた事が現実化するに至り、その技術の基本原理である多層パーセプトロンによるDNN(Deep Neural Network – 深層ニューラルネットワーク)について以下3ステップで学ぶ。
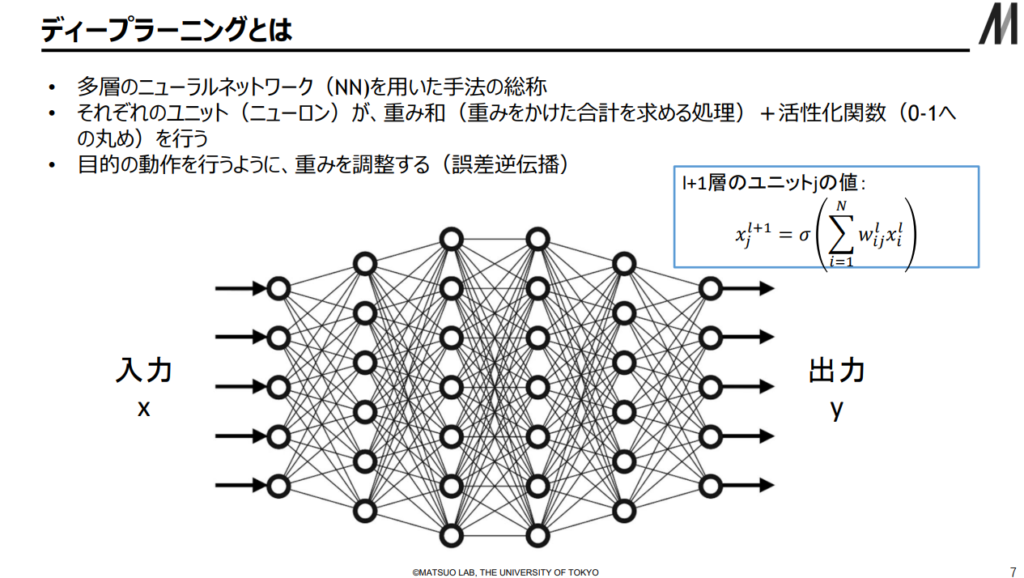
出典:AIの進化と日本の戦略 松尾研究室(23/2/17)
■第一ステップ: DNN(Deep Neural Network )の概要
・ピカソの「牛の連作」で言えばスケッチレベル。

・数式記述は最小限にとどめ、最単純誤差『逆』伝播法と非線形活性化関数(Sigmoid関数)を採用した簡単な順伝播と逆伝播(微分)の事例を紹介する。
■第二ステップ: DNNの前段階学習と位置付け
①最小二乗法 (近似解)の計算プロセス
単回帰分析(\( y_{i}=ax_{i}+b_{i}\):未知数\(a\)、\(b\)より多い連立方程式) における最小二乗法 (近似解)の計算プロセスを確認。
主な数式:行列とムーア―・ペンローズの疑似逆行列
計算結果を再度エクセルで確認。
②教師有りモデルに最小二乗法を適用した計算プロセス
主な数式:合成関数の微分(aの偏微分とbの偏微分 )と行列&逆行列
③勾配降下法による最適化(最小値)計算プロセス
逐次データを入手する毎にパラメータ(重みa、b)を更新していき、『推定値-教師データ=誤差』の『誤差二乗の合計』を次第に小さくしていき限りなく0に近づくようにして『最小値』を求める。
この手法はディープラーニングでパラメータ(重み)を計算する際に利用される。
エクセルにて勾配降下法を可視化した計算図を用意。
④ 『 3層ニューラルネットワーク』と非線形活性化関数(sigmoid)の組合せによる順伝播出力計算プロセス
各層のユニット(ニューロン)の出力計算(入力データを線形結合し、そのデータを非線形活性化関数に投入して、実数を出力(=次の層の入力データ))。
・ ピカソの「牛の連作」で言えばスケッチレベルから面レベルに拡張。

尚、最小二乗法の世界観でDNN (Deep Neural Network ) 眺めると理解もしやすくなると感じており、以下の記事を知り頷けた。
慶應義塾大学経済学部の小林慶一郎教授が日経 経済教室(2019年2月18日)で、ディープラーニング(深層学習)は、原理的には単純な最小二乗法(誤差を最小にする近似計算の一手法)にすぎない」との記事や 東京大学の松尾豊特任准教授のツィート(2019.2.19) 「ディープラーニングは最小二乗法のお化けのようなもの」「従来のマシンラーニングは(階層的に)『浅い』関数を使っていたが、ディープラーニングは『深い』関数を使っている」
■第三ステップ: 深い階層のDNN (Deep Neural Network ) を学ぶ。
・ピカソの「牛の連作」で言えば面レベルの完成を目標とする。

数式記述が中心になる。
・ 行列と合成関数の微分=連鎖律(誤差逆伝播法)について
・非線形活性化関数の特性比較(Sigmoid vs ReLU)
・損出関数の特性比較(二乗誤差関数(線形回帰)、交差エントロピー誤差(2値分類)、 交差エントロピー誤差(多値分類)
・ 『確率勾配法』や『ミニバッチ法』
尚、Andrew Glassner氏の Deep Learning: A Crash Course で氏が『誤差逆伝播法』についてbeautifulと述べらた事は今でも頭から離れない。
・ここまで理解が進めば、 Chat GPT-4のフレームワーク(Transformer)を学ぶ準備の一端が整う。
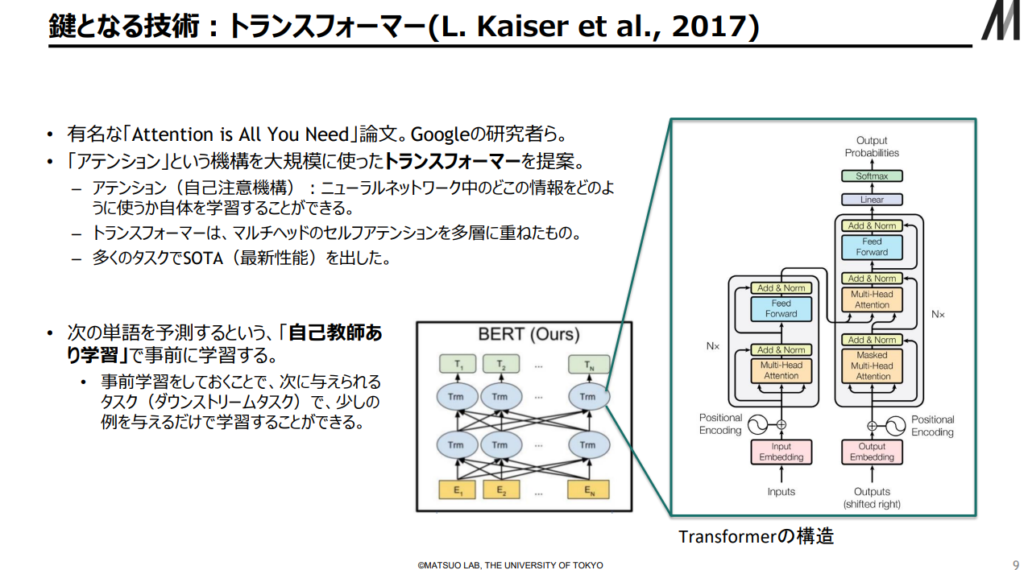
出典:AIの進化と日本の戦略 松尾研究室(23/2/17)
■■第一ステップ: DNN(Deep Neural Network )の概要■■

https://www.youtube.com/watch?v=r0Ogt-q956I
■DNN(Deep Neural Network)の簡単な仕組み
DNNとは、事前に用意した入力データ(画像、手書き文字情報等)を自ら学習する機構(多層パーセプトロン)に投入し、機構内で入力データの特徴量を自動的に抽出(=学習)させ、新規に未知の入力データがその機構に投入された際、精度の高い出力結果を判定・分類できる仕組みである。
深層ニューラルネットワーク(DNN)の目的は、最適のパラメータの発見(=学習)であり、その為に学習を繰り返す事によって予測出力を最適化するようなパラメータを導出する事である。
最適なパラメータ導出する為に、中間層(隠れ層)を多層にする事で情報伝達と処理を増やし、『特徴量』の抽出精度を上げ、出力の予測精度の向上を目指す。
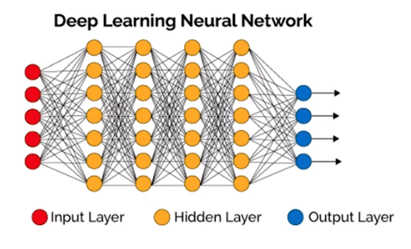
■最適なパラメータ導出の仕組みとプロセス
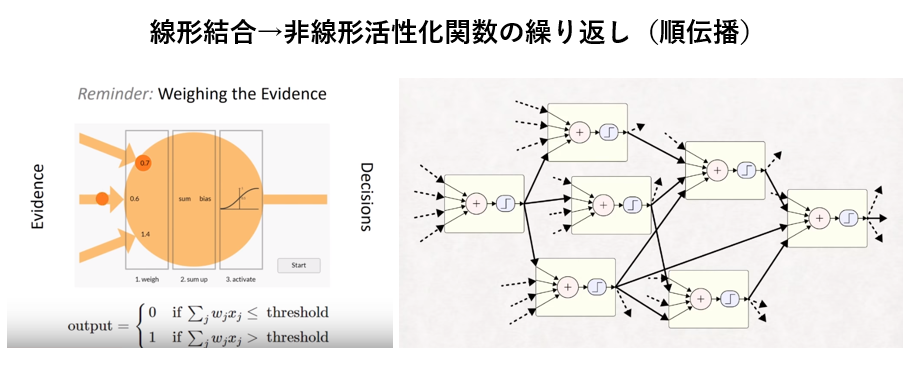
①順伝播による各層のユニット(ニューロン)の出力計算(=入力データを線形結合し、そのデータを非線形関数に投入して、実数を出力(=次の層の入力データ))。
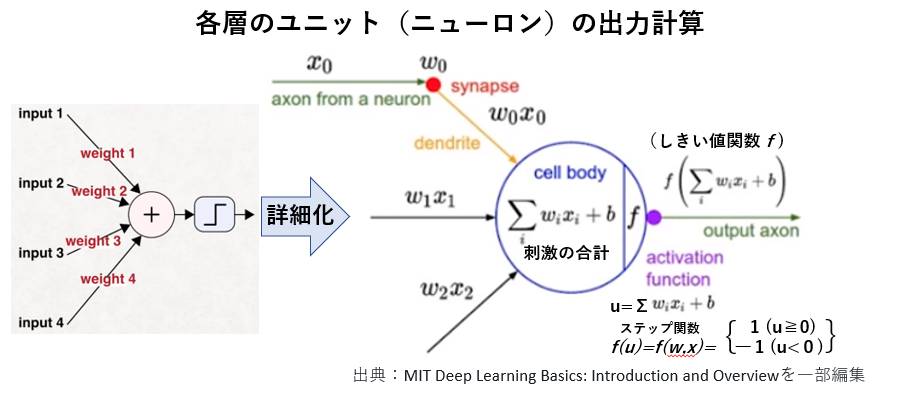
②出力層に至るまでの中間層の各ユニットは上記のプロセス(線形結合→非線形活性化関数→線形結合→非線形活性化関数→・・・・)を繰り返す。
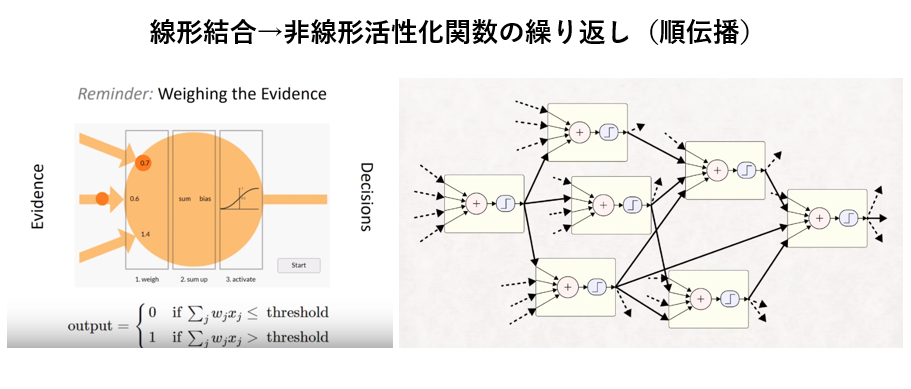
出典(右図): Deep Learning: A Crash Course
③出力層の出力値と教師データ値(=正解値)との比較による誤差値の算出。
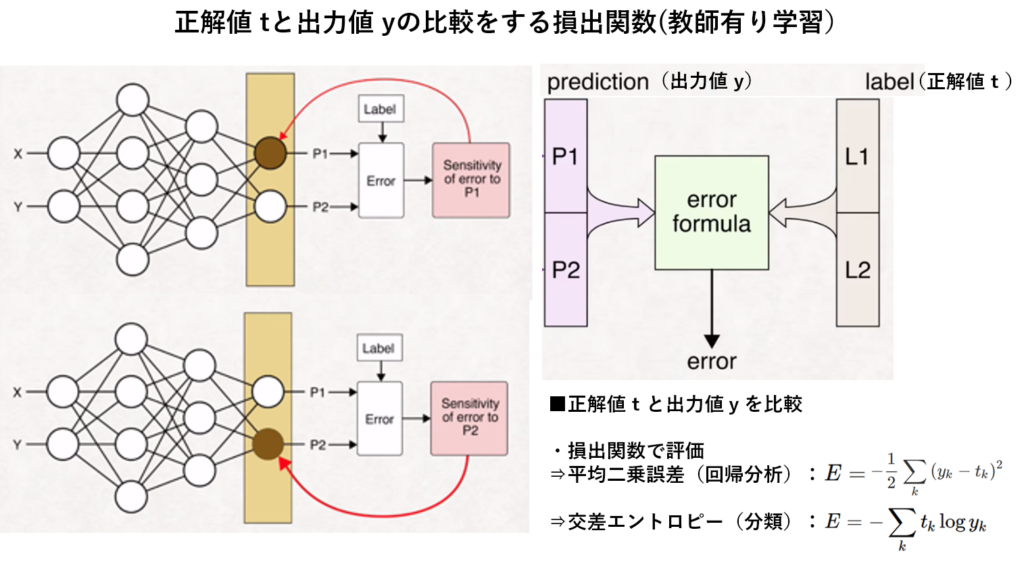
④誤差値から誤差値を最小にする逆伝播法(出力層から入力層に向かって各パラメータの更新)で学習。
⇒重みパラメータの最適解(誤差の最小値)を見出す事である。
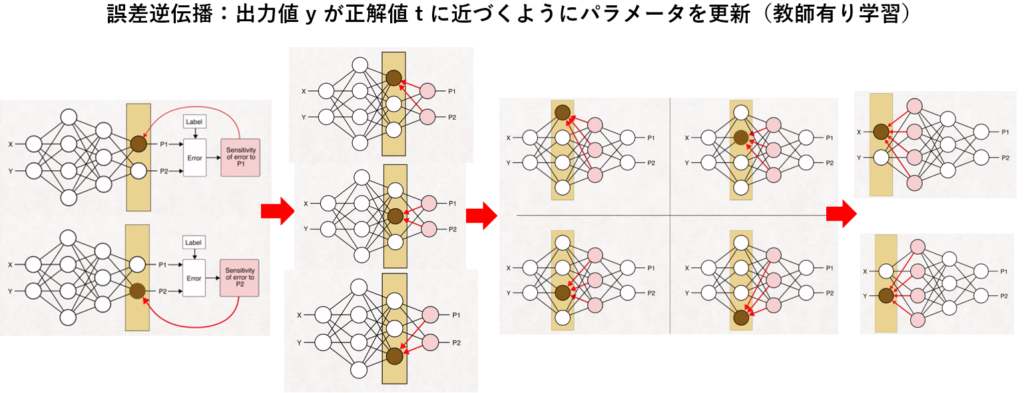
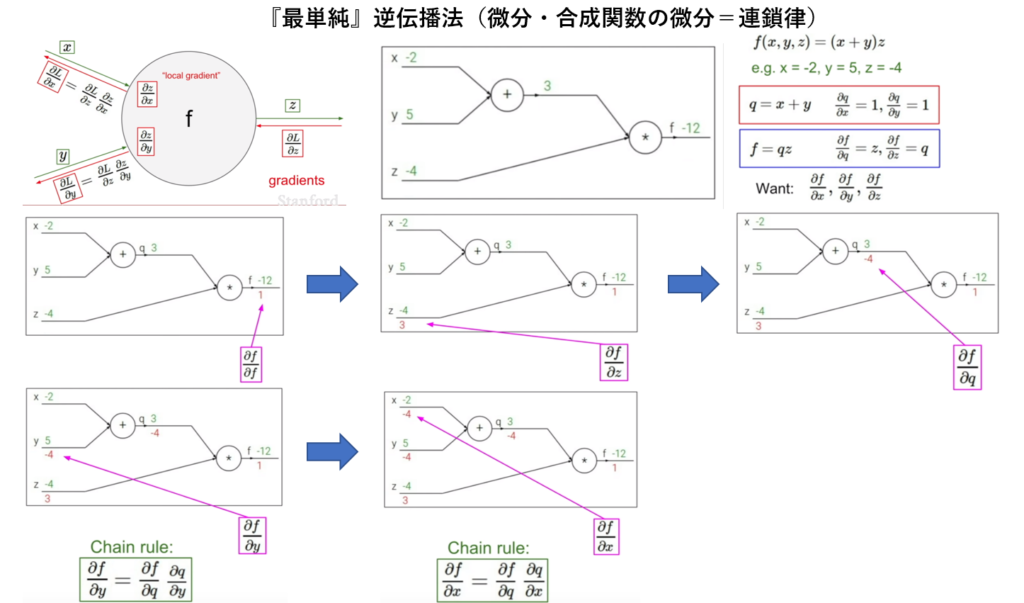
Lecture 4 | Introduction to Neural Networks
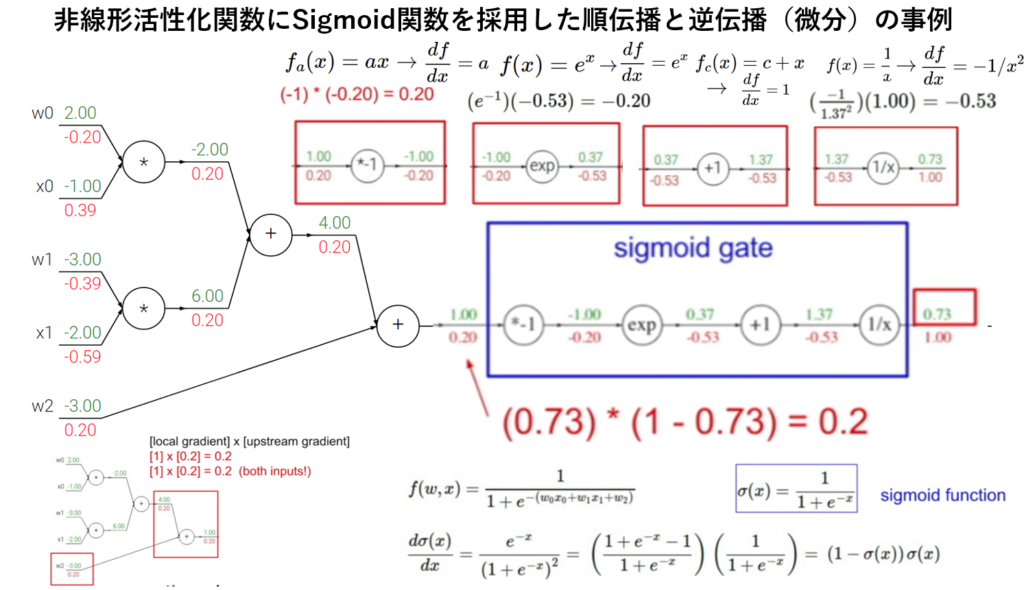
Lecture 4 | Introduction to Neural Networks
⑤上記①から④を繰り返して最適なパラメータ(最小値)を導出して学習精度の向上を図る。
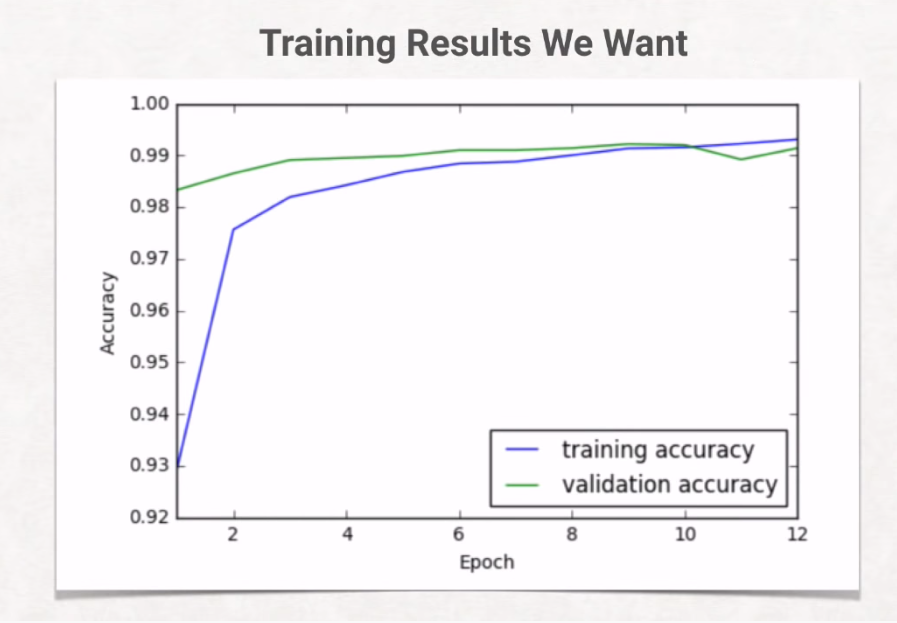
以上の流れでDNN(Deep Neural Network)の簡単な仕組みを描写した。

以下にて中身を不問にしたスケッチレベルから中身の理解を促す面レベルへとDNNについて理解の範囲を拡大する。
■■第二ステップ: 最小二乗法 (近似解)の計算プロセス(DNNの前段階学習)■■
■DNN理解のゴール■
入力情報 \( x_{1},x_{2},\ldots ,x_{m}\) から、正しい出力 \( y_{1},y_{2},\ldots ,y_{n}\) (正解)を予測する
■予測の最適化(最小値・最大値)の手法として近似解を求める最小二乗法のアイディアを『線形結合』に適用してみる。

一番簡単な単回帰直線 \( y=ax+b\)から始める。
『気温:説明変数\(x\) 』と『アイスコーヒーの注文数:目的変数 \( y\) 』のデータから気温45℃の時のアイスコーヒーの注文数を予測する。
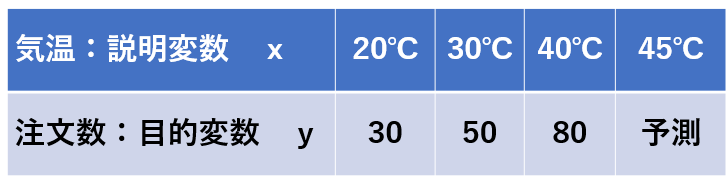
$$ \begin{aligned}20a+b=30\\ 30a+b=50\\ 40a+b=80\end{aligned} \tag { 1 } \\ $$
これを連立方程式とみると、未知数2個 (a,b)、方程式が3本なので、『解く』事が出来ない。(未知数と方程式の数は同数でなければ解けない)
同様にこの3本の方程式を行列形式で表現すると正則行列ではないので逆行列を用いた計算にて『解』を求める事が出来ない。
$$Y=XA \tag { 2 } \\ $$
\(Y=\begin{bmatrix} y_{1} \\ y_{2} \\ y_{3} \end{bmatrix}\) \(X=\begin {bmatrix} x _ { 1} , & 1 \\ x_ { 2} & 1 \\ x_{3} &1 \end{bmatrix}\) \(A=\begin{bmatrix} a \\ b \end{bmatrix}\) $$ \tag { 3 } \\$$
ここで諦めず、
『近似解』を求める事で気温45℃の時点でのアイスコーヒーの注文数を予測する。
非正則行列の場合、ムーアー・ペンローズ『擬似逆行列』を用いる事で近似解が計算出来る。早速この3式を行列形式で計算する。
\(\begin{bmatrix} 30\\ 50\\ 80\end{bmatrix}\) = \(\begin {bmatrix} 20 & 1 \\ 30 & 1 \\ 40 & 1 \end{bmatrix}\) \(\begin{bmatrix} a \\ b \end{bmatrix}\) $$ \tag { 4 } \\$$
$$Y=XA \tag { 5 } \\ $$
式(1)の両辺に左から、 \(X\) の転置行列\( X^ {T }\) を乗じる
$$X^{T}Y=X^{T}XA\ \tag { 6 } \\ $$
\(\begin{bmatrix} 20&30&40\\1&1&1\end{bmatrix}\) \(\begin {bmatrix} 30 \\50 \\80 \end{bmatrix}\) = \(\begin{bmatrix} 20&30&40\\1&1&1\end{bmatrix}\) \(\begin {bmatrix} 20 & 1 \\ 30 & 1 \\ 40 & 1 \end{bmatrix}\) \(\begin{bmatrix} a \\ b \end{bmatrix}\) $$\tag { 7 } \\ $$
\(X^{T}X\) は正方行列になるので、
これが正則行列であるならば、逆行列\( \left( X^{T}X\right) ^{-}\)が存在する
逆行列を式(2)の左から掛けると
$$ \left( X^{T}X\right) ^{-} X^{T}Y = \left( X^{T}X\right) ^{-} X^{T}XA \ \tag { 8 } \\ $$
右辺 \( A\) の前の行列演算結果は単位行列 \(E\) となるので、次式が得られる
$$ \left( X^{T}X\right) ^{-} X^{T}Y = A \tag { 9} \\ $$
尚、逆行列とは、通常の数字における逆数に対応する。例えは2の逆数は \( \dfrac {1}{2} \)になる。
つまり元の数字にかけると1を作る事ができる数字。
元の数字をかけると単位行列E(対角成分が全て1でそれ以外の成分が0であるような行列)が得られる。そんな行列の事を逆行列と呼ぶ。
EXCELにて計算結果を確認してみる
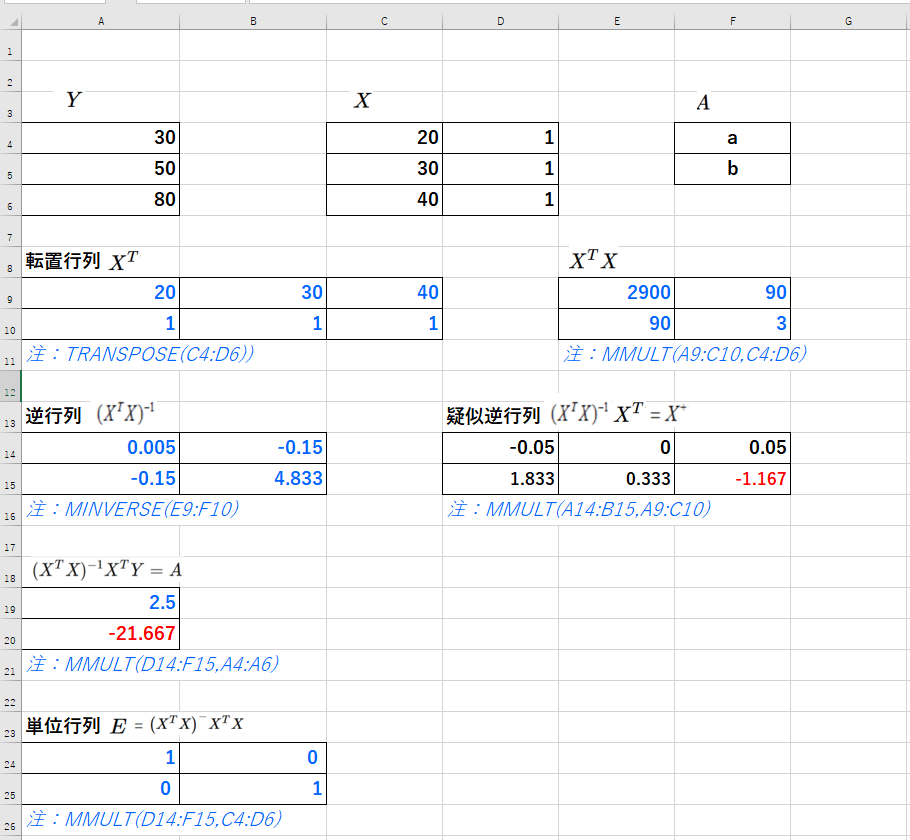
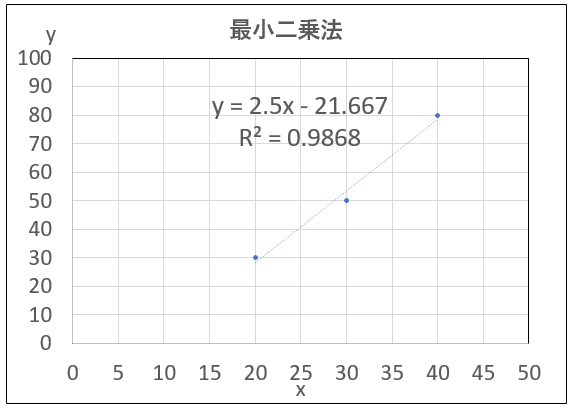
以上より3点 \( (x_{1},y_{1})\) ・・\( (x_{3},y_{3})\)をフィッティングする直線\( y=ax+b \)を求めた。
傾き\(a=2.5\)、切片\(b=-21.667\)
気温45℃の時点でのアイスコーヒーの注文数は91(=近似解)と予測出来る。
尚、最小二乗法とは、この3点の関係性を最も上手く表現するような直線を求める。すなわち近似的に解を求めようとするアプローチである。
データ点と直線の間の二乗誤差がなるべく小さくなるように未知数を定める事である。
■上記の最小二乗法の発想をDNN(Deep Neural Network)の『教師有り』モデルに照らし合わせてみると
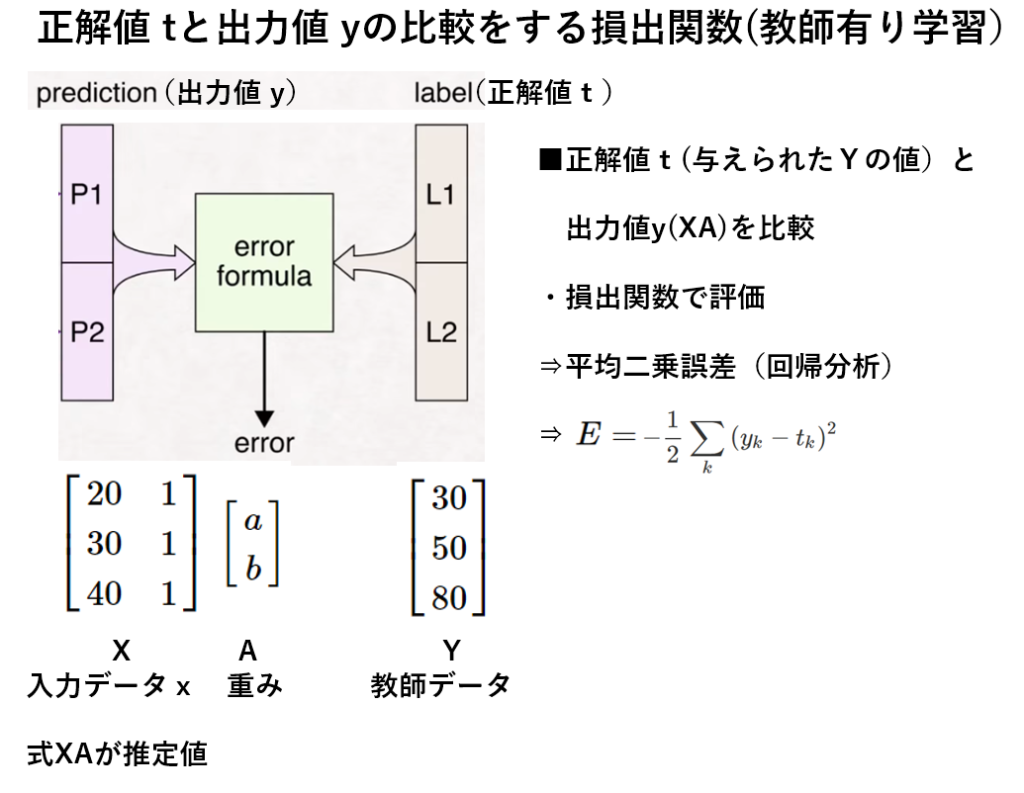
目標は、推定値(XA)と教師データ(=Y:正解値)の『差』がなるべく小さくなるように、重み(A:パラメータ)を求める事である。
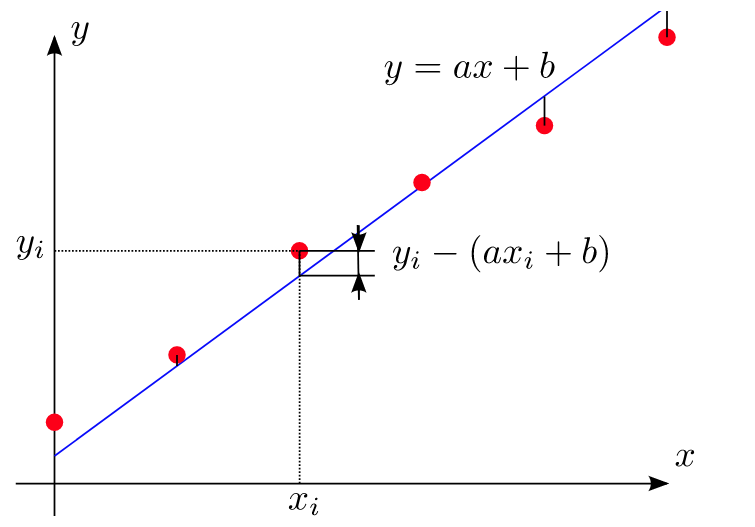
データ\( x_{i},y_{i} \)と回帰直線\( y=ax+b \) の誤差=\( y_{i} \) -\( y \)
$$ =\ y_{i}-\left( ax_{i}+b\right) \tag { 1.1 } \\ $$
次に、これらの誤差の二乗を考える。
データ\( x_{i},y_{i} \)と回帰直線\( y=ax+b \) の誤差の二乗
$$ =\left( y_{i}-\left( ax_{i}+b\right) \right) ^{2} \tag { 1.2} \\ $$
二乗する事で誤差の負の値を正の値にする。
この誤差の全てのデータ点で合計すると、 誤差の二乗の合計\(L\)
$$L= \sum_{i=1}^{{n}}(y_i-(ax_i+b))^2 \tag { 1.3 } \\ $$
と書ける。
この誤差の二乗の合計を『最小』にすることで近似回帰直線を引き、係数a、bを決める。これが最小二乗法の考えである。
\(L\)を最小にする『極値となる点では、微分した結果が0になる』ということを利用する。
$$L=\sum_{i=1}^{{n}}(y_i-ax_i-b)^2 \tag { 1.4 } \\ $$
合成関数の微分:\(a\)の偏微分
$$ \dfrac {\partial L}{\partial a}=\dfrac {\partial L}{\partial u}\dfrac {\partial u}{\partial a} \tag { 1.5 } \\ $$
$$L=(y_i-ax_i-b)^2 \tag { 1.6 } \\ $$
\(u= (y_i-ax_i-b)\) と置く(1)
$$ \dfrac {\partial L}{\partial u}=\left( u^{2}\right) ‘ \\ = 2u \tag { 1.7 } \\ $$
\(u = (y_i-ax_i-b)\)
$$ \dfrac {\partial u}{\partial a}=-x_{i} \tag { 1.8 } \\ $$
$$ \dfrac {\partial L}{\partial a}=\dfrac {\partial L}{\partial u}\dfrac {\partial u}{\partial a} \tag { 1.9 } \\ $$
$$ = 2u\cdot -x_{i}\\ = 2 (y_i-ax_i-b)\cdot -x_{i}\ $$
$$ \dfrac {\partial L}{\partial a}=-2\sum ^{n}_{i=1}x_{i}\left( y_{i}-ax_{i}-b_{i}\right) \tag { 1.10 } \\ $$
合成関数の微分:\(b\)の偏微分
$$ \dfrac {\partial L}{\partial b}=\dfrac {\partial L}{\partial u}\dfrac {\partial u}{\partial b} \tag { 1.11 } \\ $$
$$L=(y_i-ax_i-b)^2 \tag { 1.12 } \\ $$
\(u= (y_i-ax_i-b)\) と置く(1)
$$ \dfrac {\partial L}{\partial u}=\left( u^{2}\right) ‘ \\ = 2u \tag { 1.13 } \\ $$
\(u = (y_i-ax_i-b)\)
$$ \dfrac {\partial u}{\partial b}=-1 \tag { 1.14 } \\ $$
$$ \dfrac {\partial L}{\partial b}=\dfrac {\partial L}{\partial u}\dfrac {\partial u}{\partial b} \tag { 1.15 } \\ $$
$$ = 2u\cdot -1\\ = 2 (y_i-ax_i-b)\cdot -1\ $$
$$ \dfrac {\partial L}{\partial b}=-2\sum ^{n}_{i=1}\left( y_{i}-ax_{i}-b_{i}\right) \tag { 1.16 } \\ $$
係数\(a\)と\(b\)の偏微分が求まった。これらを整理する。
$$ \dfrac {\partial L}{\partial a}=-2\sum ^{n}_{i=1}x_{i}\left( y_{i}-ax_{i}-b_{i}\right) \tag { 1.17 } \\ $$
$$ \dfrac {\partial L}{\partial b}=-2\sum ^{n}_{i=1}\left( y_{i}-ax_{i}-b_{i}\right) \tag { 1.18 } \\ $$
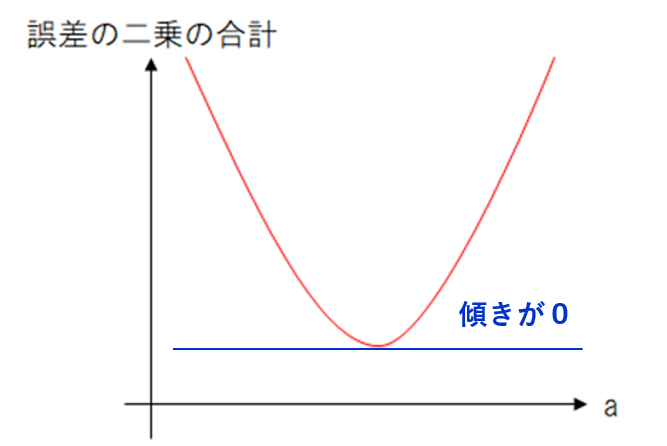
誤差の二乗の合計を『最小』にするには、傾きが『0』となる点の\(a\)を見出す事である。\(b\)も同様である。つまり\(a\)と\(b\)を偏微分してそれが『0』となる式をつくればよい。
$$ -2\sum ^{n}_{i=1}x_{i}\left( y_{i}-ax_{i}-b_{i}\right)\ = 0\ \tag { 1.19 } \\ $$
$$ -2\sum ^{n}_{i=1}\left( y_{i}-ax_{i}-b_{i}\right)\ = 0\ \tag { 1.20 } \\ $$
ここで誤差の二乗の合計\(L\)(1.3)に係数\( \dfrac {1}{2} \)を追加する(1.3-1)。
$$L= \dfrac {1}{2} \sum_{i=1}^{{n}}(y_i-(ax_i+b))^2 \tag { 1.3-1 } \\ $$
式1.19と1.20は式1.21と1.22になる。
係数\( \dfrac {1}{2} \)が付いていても、損出関数の大小関係は崩れないので問題がない。偏微分の際に肩の2乗が降りてくるのを係数で相殺できるため、式を簡単にする事ができる。
以下が\(a\)と\(b\)に関する連立方程式になる。
$$ a\sum ^{n}_{i=1}x _{i} ^{2}+b\sum ^{n}_{i=1}x_{i}=\sum ^{n}_{i=1}x_{i}y_{i} \tag { 1.21 } \\ $$
$$ a\sum ^{n}_{i=1}x_{i}+b\sum ^{n}_{i=1}1=\sum ^{n}_{i=1}y_{i} \tag { 1.22 } \\ $$
\(L\)は下に凸な二次関数なのでこれで最小値が決まる。その理由は \(a \)の後の係数\(x^{2}_{i} \)が二乗なので必ず正だからである。
以下 第三ステップを意識して 。
式\(1.21\)と\(1.22\)を行列で表す。
$$ \begin{pmatrix} \sum ^{n}_{i=1}x^{2}_{i} & \sum ^{n}_{i=1}x_{i} \\ \sum ^{n}_{i=1}x_{i} & \sum ^{n}_{i=1}1 \end{pmatrix}\begin{pmatrix} a \\ b \end{pmatrix}=\begin{pmatrix} \sum ^{n}_{i=1}x_{i}y_{i} \\ \sum ^{n}_{i=1}y_{i} \end{pmatrix} \tag { 2.1 } \\ $$
各行列を簡略化して表すと
$$XA=Y \tag { 2.2 } \\ $$
\(X\)が逆行列\(X^{-} \)を持つならば(正則行列)、式\(2.2\)の両辺に左側から \(X^{-} \) を乗じて
$$ X^{-} XA = X^{-}Y \tag { 2.3 } \\ $$
ここで
$$ X^{-} X = E \tag { 2.4 } \\ $$
\(E\)は単位行列。よって式\(2.3\)は下記になる。
$$ A = X^{-}Y \tag { 2.5 } \\ $$
$$ \begin{aligned}\begin{pmatrix} a \\ b \end{pmatrix}=\begin{pmatrix} \sum ^{n}_{i=1}xi^{2} & \sum ^{n}_{i=1}x_{i} \\ \sum ^{n}_{i=1}x_{i} & \sum ^{n}_{i=1}1 \end{pmatrix}^{-}\begin{pmatrix} \sum ^{n}_{i=1}x_{i}y_{i} \\ \sum ^{n}_{i=1}y_{i} \end{pmatrix}\\ \end{aligned} \tag { 2.6 } \\ $$
逆行列の公式より
$$ X ^{-} =\begin{pmatrix} a & b \\ c & d \end{pmatrix}^{-}=\dfrac {1}{ad-bc}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix} \tag { 2.7 } \\ $$
式\(2.6\)に式\(2.7\)の\(X ^{-} \)を適用する
ここで
$$ \Delta =\sum ^{n}_{i=1}1\sum ^{n}_{i=1}x^{2}_{i}-\left( \sum ^{n}_{i=1}x_{i}\right) ^{2} $$
とすると
$$ \begin{pmatrix} a \\ b \end{pmatrix}=\dfrac {1}{\Delta }\begin{pmatrix} \sum ^{n}_{i=1}1 & -\sum ^{n}_{i=1} x_{i} \\ -\sum ^{n}_{i=1} x_{i} & \sum ^{n}_{i=1} x^{2}_{i} \end{pmatrix}\begin{pmatrix} \sum ^{n}_{i=1} x_{i}y_{i} \\ \sum ^{n}_{i=1} y _{i} \end{pmatrix} \tag { 2.8 } \\ $$
最小二乗法で得られる傾き\(a\)と切片\(b\)が分かる。
$$ a=\dfrac {\sum 1\sum x_{i}y_{i} -\sum x_{i}\sum y_{i}}{\sum 1\sum x^{2}_{i}-\left( \sum x_{i}\right) ^{2}} \tag { 2.9 } \\ $$
$$ b=\dfrac {-\sum x_{i}\sum x_{i}y_{i}+\sum x^{2}_{i}\sum y_{i}}{\sum 1\sum x^{2}_{i}-\left( \sum x_{i}\right) ^{2}} \tag { 2.10 } \\ $$
但し、\(Σ\)は\(i=1,2,・・,n\)とする。\(n\)はデータ数
$$ x_{1}=20,x_{2}=30,x_{3}=40 $$
$$ y_{1}=30,y_{2}=50,y_{3}=80 $$
より、上記\(a\)、\(b\)の式に代入すると結果は以下になる。
$$ a=2.5 $$
$$ \sum 1\sum x_{i}y_{i} =( 20×30 +30×50 +40×80 )×3 = 15900 $$
$$ \sum x_{i}\sum y_{i} =( 20+30+40)×(30+50+80) = 14400 $$
$$ \sum 1\sum x^{2}_{i} =(20^2+30^2+40^2) ×3 = 8700 $$
$$ \left( \sum x_{i}\right) ^{2} = (20+30+40)^2 = 8100 $$
$$ \dfrac {15900-14400}{8700-8100}=\dfrac {1500}{600}=2.5 $$
$$ b=-21.667 $$
$$ \sum x_{i}\sum x_{i}y_{i} = (20+30+40)*( 20×30 +30×50 +40×80 ) = 477000 $$
$$ \sum x^{2}_{i}\sum y_{i} =(20^2+30^2+40^2) × (30+50+80) = 46400 $$
$$ \sum 1\sum x^{2}_{i} =(20^2+30^2+40^2) ×3 = 8700 $$
$$ \left( \sum x_{i}\right) ^{2} = (20+30+40)^2 = 8100 $$
$$ \dfrac {-477000+464000}{8700-8100}=\dfrac {-13000}{600}=-21.667 $$
第三ステップに向けて(深い階層のDNN (Deep Neural Network ) を学ぶ)
■勾配降下法
最適化(最大値・最小値)についてのアプローチとして既に①ムーア―・ペンローズ『疑似逆行列』、②最小二乗法にて最小値を求めた。
今回、『勾配降下法』で 「気温:説明変数x 」と「アイスコーヒーの注文数:目的変数 y 」のデータを流用して最小値を求める。
$$ \begin{aligned}20a+b=30\\ 30a+b=50\\ 40a+b=80\end{aligned} \tag { 1 } \\ $$
『勾配降下法』の手法は、逐次データを入手する毎にパラメータ(重みa、b)を更新していき、『推定値-教師データ=誤差』の『誤差二乗の合計』を次第に小さくしていき限りなく0に近づくようにして『最小値』を求める。
別の表現で言うと 合成関数の微分\(a\)の偏微分値と\(b\)の偏微分値が0(限りなく0)になる事である。
概念はボール(初期値の重みaとb)が谷底に向かって落下していくイメージである。
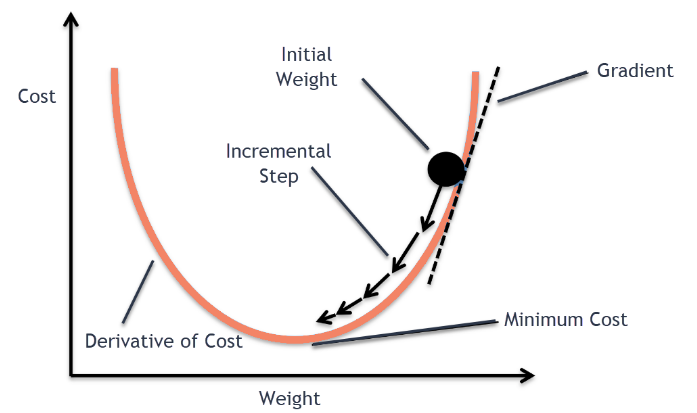
具体的なボールの動きの様子は、エクセルにて勾配降下法を可視化した計算図を後段で用意しています。
増分ステップの動きは現状の重みaとbから『勾配ΔL×学習率η(移動距離aとb) の欄の数値データ』を引いた値になります。
$$ \ W^{\left( t+1\right) }\leftarrow W^{\left( t\right) }-\eta \dfrac {\partial E}{\partial w} \\ $$
この手法はディープラーニングでパラメータ(重み)を計算する際に利用される。
尚、既に②において 誤差二乗の合計を『最小』にすることで近似回帰直線を引き、係数a、bを決める際に行った合成関数の微分(aの偏微分値 とbの偏微分値)が『勾配降下法』にて再利用できる。
【 再掲示】誤差の二乗の合計を『最小』にするには、傾きが『0』となる点の\(a\)を見出す事である。\(b\)も同様である。つまり\(a\)と\(b\)を偏微分してそれが『0』となる式をつくればよい。
合成関数の微分:\(a\)の偏微分
$$ \dfrac {\partial L}{\partial a}=-2\sum ^{n}_{i=1}x_{i}\left( y_{i}-ax_{i}-b_{i}\right) \tag { 1.17 } \\ $$
$$ -2\sum ^{n}_{i=1}x_{i}\left( y_{i}-ax_{i}-b_{i}\right)\ = 0\ \tag { 1.19 } \\ $$
合成関数の微分:\(b\)の偏微分
$$ \dfrac {\partial L}{\partial b}=-2\sum ^{n}_{i=1}\left( y_{i}-ax_{i}-b_{i}\right) \tag { 1.18 } \\ $$
$$ -2\sum ^{n}_{i=1}\left( y_{i}-ax_{i}-b_{i}\right)\ = 0\ \tag { 1.20 } \\ $$
ここで誤差の二乗の合計\(L\)(1.3)に係数\( \dfrac {1}{2} \)を追加する(1.3-1)。
$$L= \dfrac {1}{2} \sum_{i=1}^{{n}}(y_i-(ax_i+b))^2 \tag { 1.3-1 } \\ $$
係数\( \dfrac {1}{2} \)が付いていても、損出関数の大小関係は崩れないので問題がない。偏微分の際に肩の2乗が降りてくるのを係数で相殺できるため、式を簡単にする事ができる。
勾配降下法で最小値を求める計算式は以下を繰り返すだけである。
$$ \ a_{next}=a_{prev}-\eta \dfrac {\partial L}{\partial a} \tag { 3.1 } \\ $$
$$ \ a_{next}=a_{prev}-\eta \ x_{i}\left( ax_{i}+b_{i} – y_{i}\right)\ \tag { 3.2 } \\ $$
$$ \ b_{next}=b_{prev}-\eta \dfrac {\partial L}{\partial b} \tag { 3.3 } \\ $$
$$ \ b_{next}=b_{prev}-\eta \ \left( \ ax_{i}+b_{i} – y_{i}\right)\ \tag { 3.4 } \\ $$
η:学習率。この値の設定(小数点以下の桁数設定)で誤差二乗の合計値が発散する場合がある。誤差二乗の合計が小さく(収束)なるように小数点以下の桁数設定に注意を払う必要がある。
尚、Deep Neural Networkで紹介されている勾配降下法の計算式は以下である。
t回目の重み更新式(勾配降下法)
$$ \ W^{\left( t+1\right) }\leftarrow W^{\left( t\right) }-\eta \dfrac {\partial E}{\partial w} \\ $$
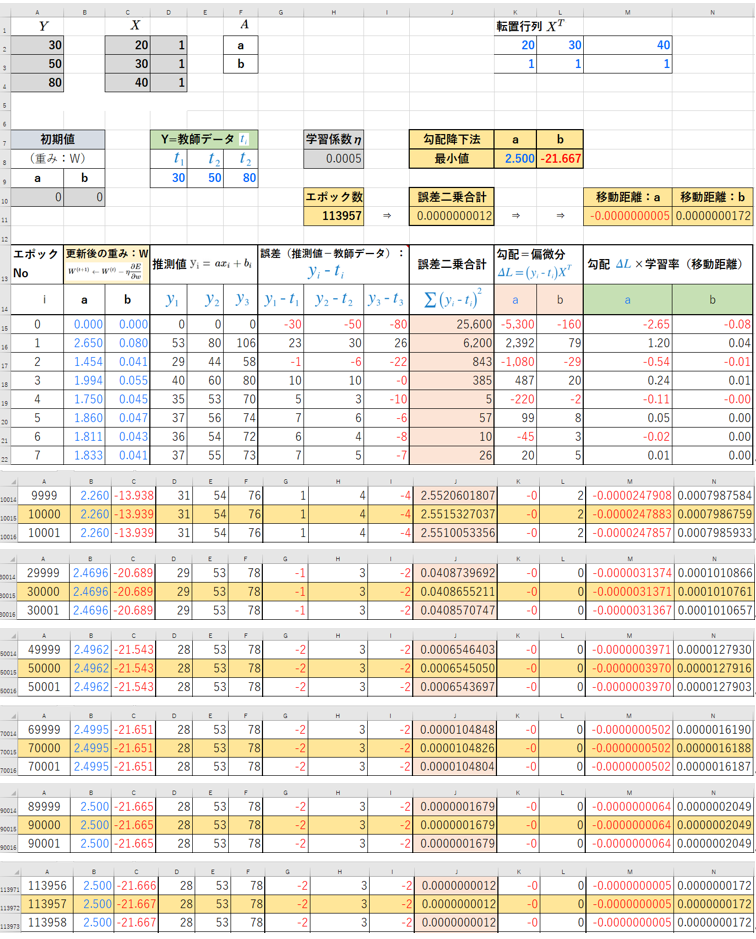
実際、エクセルにて勾配降下法を可視化してみる。
学習率η:0.0005、初期値の重みa:0、b:0で式(3.2)及び(3.4)を使い計算した結果、
最小値a:2.500、b:-21.667を得るために要したエポック数は113,957になる。
その時の誤差二乗合計値:0.0000000012
勾配ΔL×学習率(移動距離)a:-0.0000000005、b:0.0000000172であった。
勾配降下法は収束スピードが導関数に依存しており、微分係数が0に近いと収束が極めて遅くなることがエクセルで確認できる。(エポック数113,957)
■勾配降下法の欠点
多層パーセプトロンで構成されたDNNは、線形結合→非線形活性化関数→線形結合→非線形活性化関数・・・の繰り返しで構成されており、損出関数は非常に複雑な非凸関数になる。
出典(右図): Deep Learning: A Crash Course
その為、大域的極小値(真の最小値)以外にも局所的最小値が多数存在する。
勾配降下法を用いて、損出関数の最小化を繰り返すとこの局所的最小値に入ってしまい大域的極小値(真の最小値)に辿り着けない事がある。
更に、エクセルにて勾配降下法を可視化した際の収束スピードの問題点も挙げられる。
加えて勾配降下法はパラメータ(変数)が増えるにつれて計算量が膨れ上がる弱点もある。一例として重回帰分析の変数。
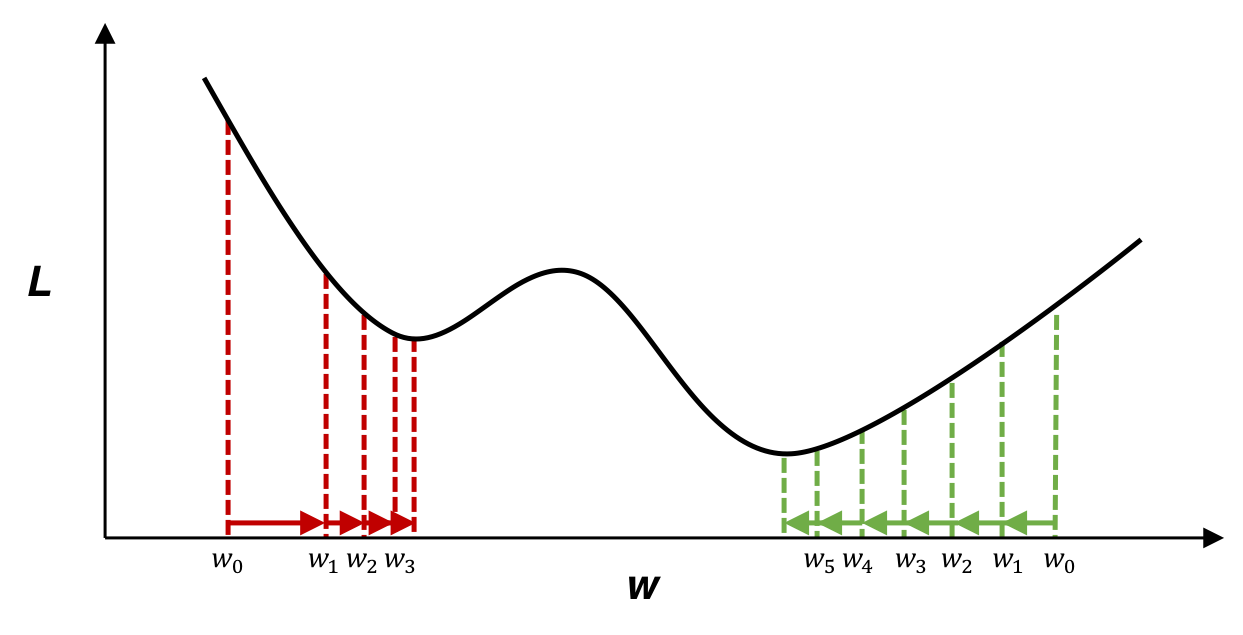
https://axa.biopapyrus.jp/deep-learning/gradient_descent_method.html
第三ステップでこれらの弱点を克服する手法として『確率勾配法』や『ミニバッチ法』を学ぶ。
■ムーアー・ペンローズ『擬似逆行列』 の価値を再確認する。
逆行列の計算では
行数と列数が等しい正方行列のみ計算が可能である事を
誤差の二乗の合計\(L\) を最小にする計算プロセスで確認した。
具体的には式\(1.21、1.22\)を行列形式で表した式\(2.1\)である。
$$ \begin{pmatrix} \sum ^{n}_{i=1}x^{2}_{i} & \sum ^{n}_{i=1}x_{i} \\ \sum ^{n}_{i=1}x_{i} & \sum ^{n}_{i=1}1 \end{pmatrix}\begin{pmatrix} a \\ b \end{pmatrix}=\begin{pmatrix} \sum ^{n}_{i=1}x_{i}y_{i} \\ \sum ^{n}_{i=1}y_{i} \end{pmatrix} \tag { 2.1 } \\ $$
しかし、下記のように\(n\)個の未知数(\( a、b\))に対して、式が\( m \)本(\(m>n\))ある場合、逆行列を使って解くことができない事は式\((1\))~\((9\))で最初に紹介した。
$$Y=XA \tag { 2 } \\ $$
\(\begin{bmatrix} 30\\ 50\\ 80\end{bmatrix}\) = \(\begin {bmatrix} 20 & 1 \\ 30 & 1 \\ 40 & 1 \end{bmatrix}\) \(\begin{bmatrix} a \\ b \end{bmatrix}\) $$ \tag { 4 } \\$$
行列Xの行数が列数よりも多い時(未知数よりもデータ数が多い時)、ムーア・ペンローズ疑似逆行列を使って、行列Aに関して近似的に解く事が可能となる事を \((1\))~\((9\)) で確認した。
正方行列でなくとも近似解ではあるが逆行列のように扱え、一発で解が求まる点に価値がある。
■『 3層ニューラルネットワーク順伝播』と『ニューロンと重みの表記』& 行列の乗算と転置及び加減
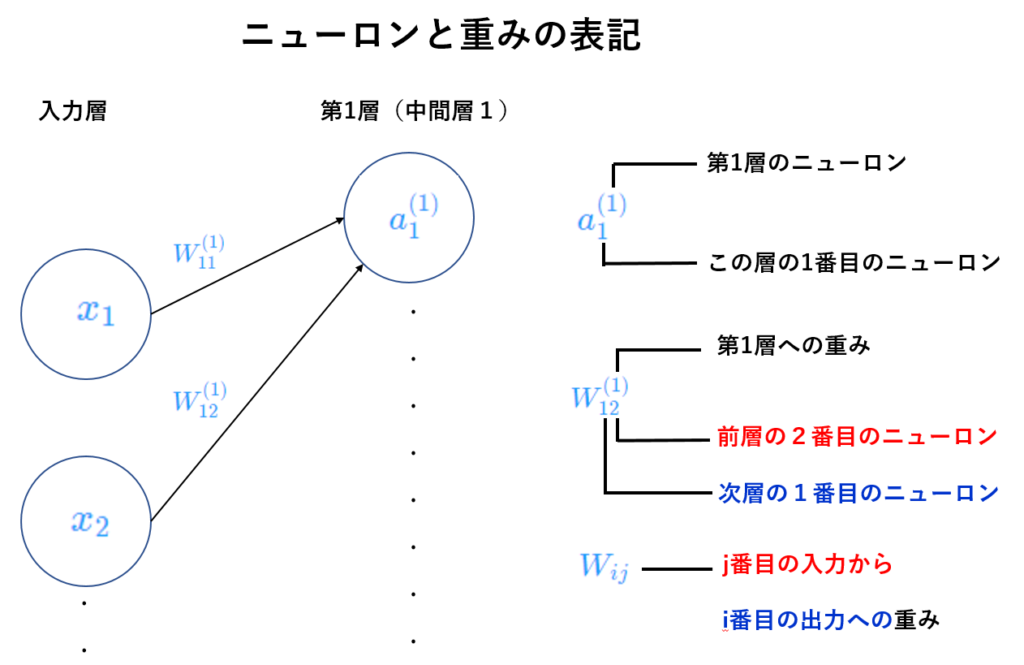
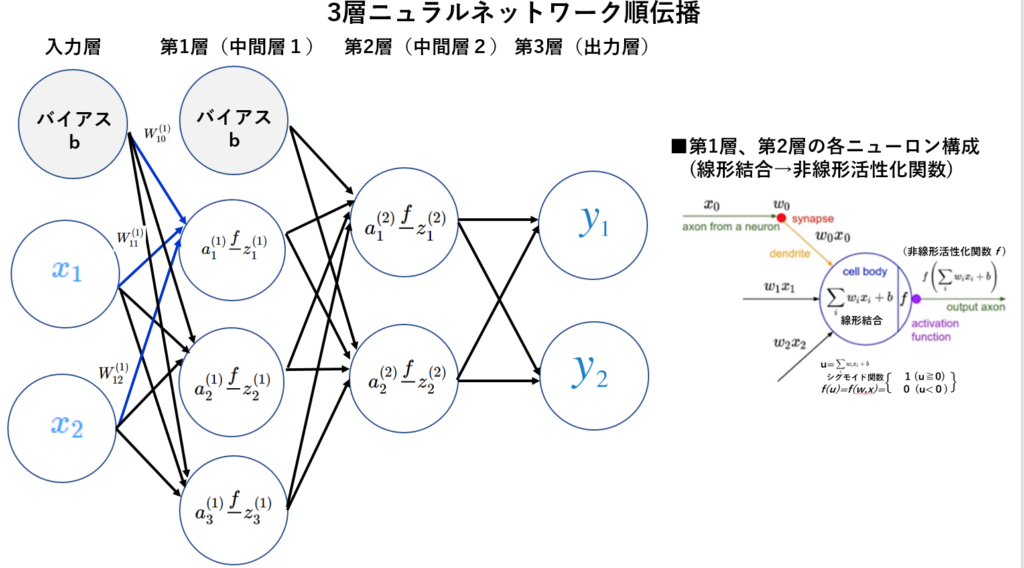
①\(j\)番目の入力から \( i \) 番目への出力の重み
$$ w_{ij} $$
\( i \) は次の層のニューロンのインディクスを示す。
『次層のニューロン番号、前層のニューロン番号』という並び順。
$$ W^{\left( 1\right) }_{11} \\ $$
上記の重み表記は
前層の1番目のニューロンから
次層(第1層)の1番目ニューロンへの重み
$$ W^{\left( 1\right) }_{12} \\ $$
上記の重み表記は、
前層の2番目のニューロンから
次層(第1層)の1番目ニューロンへの重み
つまり \(a^{\left( 1\right) }_{1} \) への重みである事を意味する。
②中間層\(l \)の\( i \) 番目のニューロンに対する入力
$$ a^ {\left( l\right) }_{i} \left( = \sum wx+b\right) \\ $$
③非線形活性化関数
$$ f \\ $$
④中間層\(l \)の\( i \) 番目のニューロンに対する出力
$$ Z^{\left( l\right) }_{i} \\ $$
⑤ニューロンの構成内容
$$ a^{\left( l\right) }_{i}\dfrac {f}{}z ^{\left( l\right) } _{i} \\ $$
◇行列の乗算と転置及び加減
●行列の乗算
行列の乗算では、行列同士を掛け合わせて新しい行列を求める為の規則がある。
規則
全ての行列で乗算を行えるわけではない。更に結果の行列の次元に関する規定がある。
1.1つの目の行列の列数と2つ目の行列の行数が同じである
2.M×N行列とN×K行列の積はM×K行列である。
新しい行列の行数は1つ目の行列の行数、列数は2つ目の行列の列数となる。
<内積>
$$ \begin{bmatrix} a & b \\ c & d \\ e & f \end{bmatrix}\cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}=\begin{bmatrix} 1a+3b & 2a+4b \\ 1c+3d & 2c+4d \\ 1e+3f & 2e+4f \end{bmatrix} \\ $$
<行列のアダマル積>
行列のアダマル積は、要素毎の演算。対応する位置の値を掛け合わせて新しい行列を求める。
$$ \begin{bmatrix} a_{1} & a_{2} \\ a_{3} & a_{4} \end{bmatrix}\odot \begin{bmatrix} b_{1} & b_{2} \\ b_{3} & b_{4} \end{bmatrix}=\begin{bmatrix} a_{1} \cdot b_{1} & a_{2} \cdot b _{2} , \\ a_{3}\cdot b_{3} & a_{4}\cdot b_{4} \end{bmatrix} \\ $$
注:アダマル積は誤差逆伝播法を実行する際に利用する。
<行列の転置>
行列の転置は、行列の乗算の要件を満たさない場合、乗算の要件をを満たして演算を続行できるように、行列の1つを回転する方法を提供。
転置\(\left(^{T}\right) \)は、以下の操作を表す。操作の前後で行列のサイズが変わっている事に注意。
$$ \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix}^{T}=\begin{pmatrix} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \end{pmatrix} \\ $$
<行列の加算、減算、除算>
2つの行列間で加算、減算、除算を行うには、両者の次元が同じである事が必要。
対応する要素の値を組み合わせて、新しい行列を求める。
$$ \begin{bmatrix} a & b \\ c & d \end{bmatrix}+\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}=\begin{bmatrix} a+1 & b+2 \\ c+3 & d+4 \end{bmatrix} \\ $$
◆1-1:第1層の入力
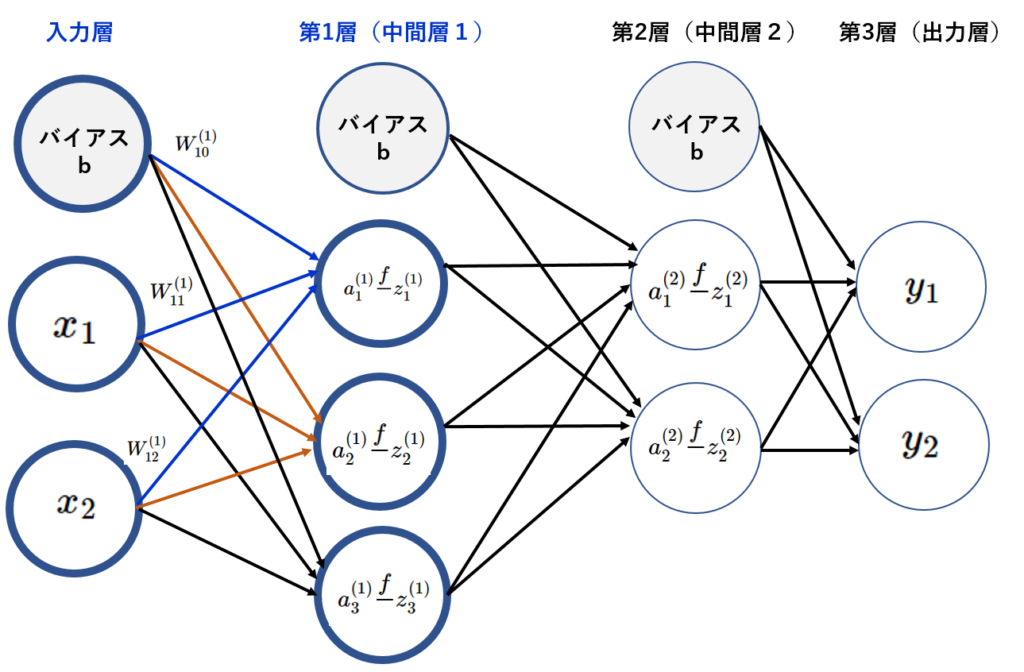
入力層の信号が第1層の
$$ a^{\left( 1\right) }_{1} $$
へ送信されるケースを取り上げる。
更に入力層のバイアス\(b\)が追加される。
$$ a^{\left( 1\right) }_{1} $$
は重み付きとバイアスの信号の和になるので、次式で表せる。
$$ a^{\left( 1\right) }_{1}= W^{\left( 1\right) }_{11}+W^{\left( 1\right) }_{12}+ W^{\left( 1\right) }_{10} \tag { 4-1} \\ $$
ここで
$$ a^{\left( 1\right) }_{1} , a^{\left( 1\right) }_{2}, a^{\left( 1\right) }_{3} $$
をまとめて計算できるように、以下の行列を定義する。
$$ A^ {\left( 1\right) } = \begin{pmatrix} a^{\left( 1\right) }_{1} & a^{\left( 1\right) }_{2} & a^{\left( 1\right) }_{3} \end{pmatrix} \\ $$
入力層の出力は
$$ X=\begin{pmatrix} x_{1} & x_{2} \end{pmatrix} \\ $$
第1層へのバイアスは
$$ b^ {\left( 1\right) } = \begin{pmatrix} W^{\left( 1\right) }_{10} & W^{\left( 1\right) }_{20} & W^{\left( 1\right) }_{30} \end{pmatrix} \\ $$
第1層への重みは
$$ W^{\left( 1\right) }=\begin{pmatrix} W^{\left( 1\right) } _ {11} & W ^ {\left( 1\right) } _{12} \\ W^ {\left( 1\right) } _{21} & W^ {\left( 1\right) } _{22} \\W^ {\left( 1\right) } _{31} & W^ {\left( 1\right) } _{32} \end{pmatrix} \\ $$
$$ W^{\left( 1\right) ^{T}}= \begin{pmatrix} W^{\left( 1\right) } _ {11}& W^ {\left( 1\right) } _{21} & W^{\left( 1\right) }_{31} \\ W^ {\left( 1\right) } _{12} & W^ {\left( 1\right) } _{22} & W^ {\left( 1\right) } _{32} \end{pmatrix} \\ $$
上記添え字\(T\)は重みの転置行列である。
尚、重みを転置行列にするのは行列の積のルールに従う。
入力層の\(X\)は1行2列、重み\(W\)は3行2列。
重み\(W\)を転置し2行3列にすると行列の積のルール通りになる。
\(X\)の列数と\(W\)の行数が一致しないといけない。(行列の積のルール①)
以上の定義により第1層が入力する『重み付き和』は次式で表せる。
$$ A^{\left( 1\right) } =XW^ {\left( 1\right) ^{T}} +b^ {\left( 1\right) } \tag { 4-2} \\ $$
第1層の重み付き和の入力値を計算する。
入力層の出力\(X\)、重み\(W\)、バイアス\(b\)に値を以下のように設定。
$$ X=\begin{pmatrix} x_{1} & x_{2} \end{pmatrix}=\begin{pmatrix} 1.0 & 0.5 \end{pmatrix} \\ $$
$$ W^{\left( 1\right) }=\begin{pmatrix} W^{\left( 1\right) } _ {11} & W ^ {\left( 1\right) } _{12} \\ W^ {\left( 1\right) } _{21} & W^ {\left( 1\right) } _{22} \\W^ {\left( 1\right) } _{31} & W^ {\left( 1\right) } _{32} \end{pmatrix} =\begin{pmatrix}0.1 & 0.2 \\0. 3 & 0.4 \\ 0.5 & 0.6 \end{pmatrix} \\ $$
Xの行列(1行2列)と\(W ^ {\left( 1\right) } \)の行列(3行2列)の積はルール違反。
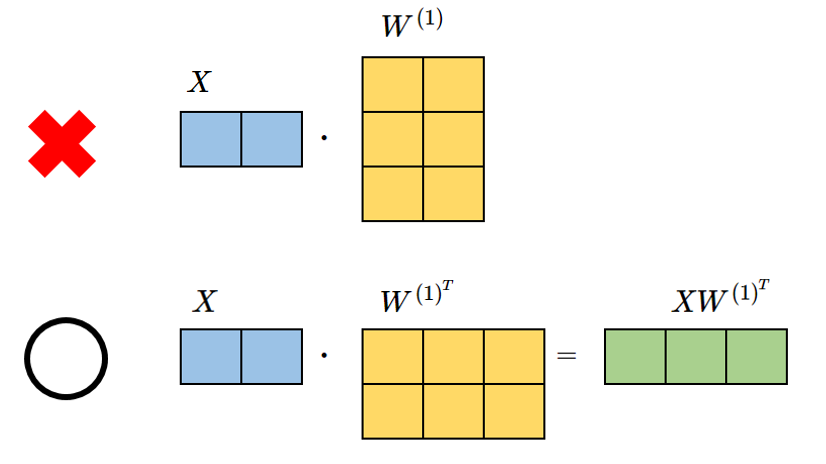
Xの行列(1行2列)、 \(W^{\left( 1\right) ^{T}}\)の行列(2行3列)になり、積の演算が出来る。
$$ W^{\left( 1\right) ^{T}}= \begin{pmatrix} W^{\left( 1\right) } _ {11}& W^ {\left( 1\right) } _{21} & W^{\left( 1\right) }_{31} \\ W^ {\left( 1\right) } _{12} & W^ {\left( 1\right) } _{22} & W^ {\left( 1\right) } _{32} \end{pmatrix} =\begin{pmatrix} 0.1 & 0.3 & 0.5 \\ 0.2 &0. 4 &0. 6 \end{pmatrix} \\ $$
$$ XW ^ {\left( 1\right) ^{T}} = \begin{pmatrix} 1.0 & 0.5 \end{pmatrix} \begin{pmatrix} 0.1 &0. 3 & 0.5 \\0. 2 & 0.4 & 0.6 \end{pmatrix} \\ $$
$$ XW ^ {\left( 1\right) ^{T}} = \begin{pmatrix} 0.2 & 0.5 & 0.8 \end{pmatrix} \\ $$
\(X\)の列数と\(W\)の行数が一致しないといけない。(行列の積のルール①)
積を取った後の行列サイズに注意。
\(k\)×\(m\)行列と \(m\)×\(n\) の積を取ると\(k\)×\(n\)行列になる。(行列の積のルール②)
$$ b^ {\left( 1\right) } = \begin{pmatrix} W^{\left( 1\right) }_{10} & W^{\left( 1\right) }_{20} & W^{\left( 1\right) }_{30} \end{pmatrix} = \begin{pmatrix} 0.1 &0. 2 & 0.3 \end{pmatrix} \\ $$
$$ A^{\left( 1\right) } =XW^ {\left( 1\right) ^{T}} +b^ {\left( 1\right) } \tag { 4-2 } \\ $$
$$ A^{\left( 1\right) } = \begin{pmatrix} 0.2 & 0.5 & 0.8 \end{pmatrix} + \begin{pmatrix} 0.1 &0. 2 & 0.3 \end{pmatrix} \\ $$
$$ A^{\left( 1\right) } = \begin{pmatrix} 0.3 & 0.7 & 1.1 \end{pmatrix} \\ $$
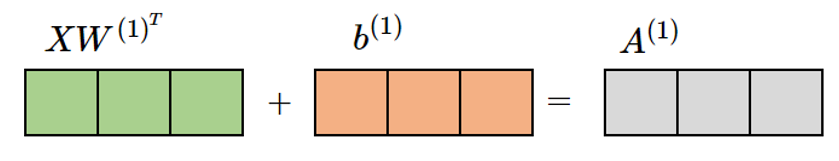
行列の和は同じ位置の要素同士を足すだけである。和を取る行列サイズは同じでなければならない(行列の和のルール)
これが第1層の入力値になる。
$$ A^ {\left( 1\right) } = \begin{pmatrix} a^{\left( 1\right) }_{1} & a^{\left( 1\right) }_{2} & a^{\left( 1\right) }_{3} \end{pmatrix} \\ $$
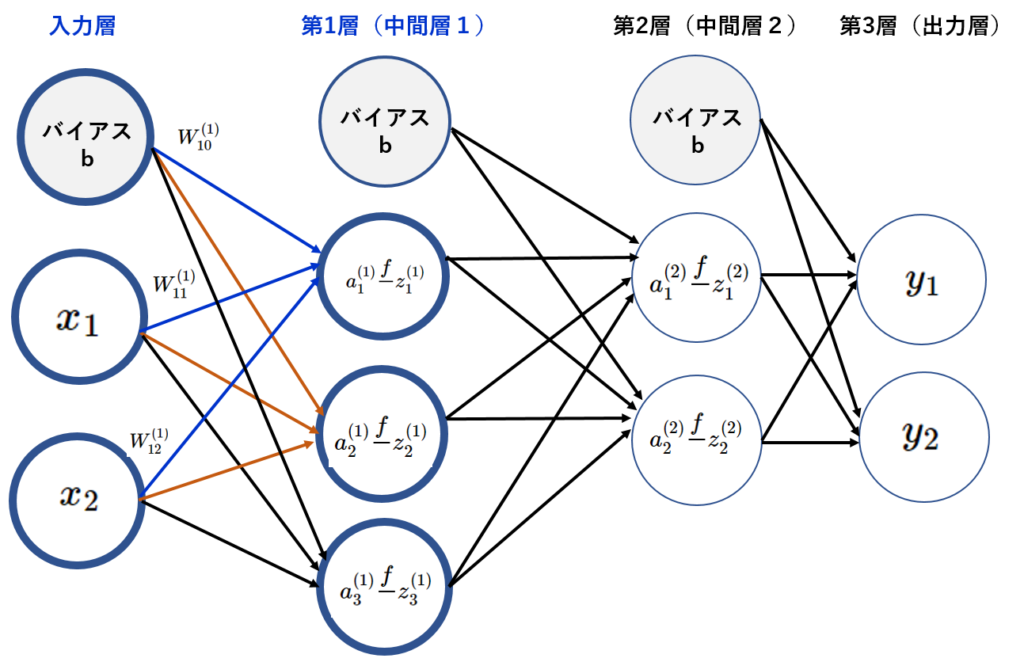
◆1-2:第1層からの信号を出力する。
非線形活性化関数(シグモイド関数)の出力値を第1層の出力とする。
$$ f\left( a\right) =\dfrac {1}{1+\exp \left( -a\right) } \tag { 4-3} \\ $$
上記式に
$$ A^{\left( 1\right) } = \begin{pmatrix} 0.3 & 0.7 & 1.1 \end{pmatrix} \\ $$
の値を代入する。
$$ Z^ {\left( 1\right) } = \begin{pmatrix} z^{\left( 1\right) }_{1} & z^{\left( 1\right) }_{2} & z^{\left( 1\right) }_{3} \end{pmatrix} = \begin{pmatrix} 0.57444252 & 0.66818777 & 0.75026011 \end{pmatrix} \\ $$
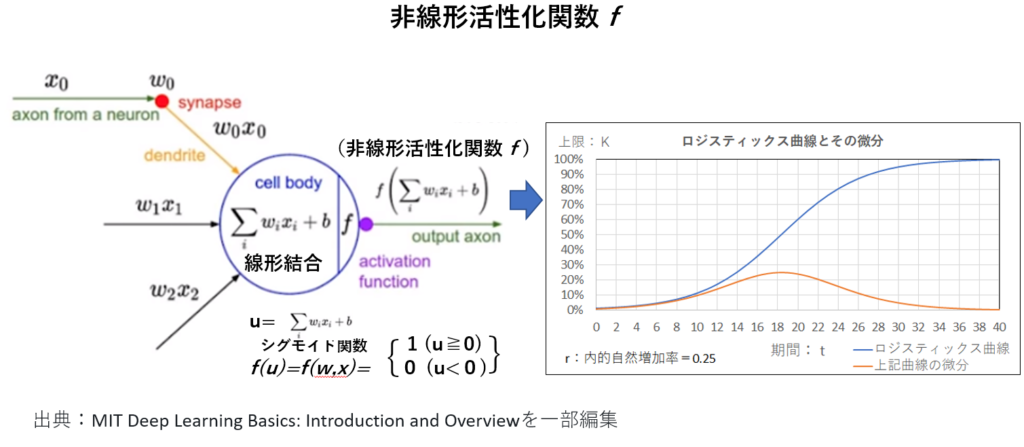
上図の右図にてシグモイド関数の特性を表示。
シグモイド関数は誤差逆伝播の際、微分すると最大値が0.25になり、微分を繰り返すと(前の層に伝播すると)0に近づく為、深い多層パーセプトロンには採用されない。
具体的には3層のニューラルネットワークの場合、最大値を取り続けても、 \(0.25^{3}≒0.016\)倍に薄まった誤差が伝播される形になる。10層になると入力層側の誤差は \(0.25^{10}≒0.000001\) 倍に薄まってしまう。
あまりにも小さな勾配しか伝わらなくなり、パラメータの更新量がほとんど0になる為、どんなに目的関数が大きくなっても、入力層に近い関数が持つパラメータは変化しなくなる。
初期値からほとんど値が変わらなくなり、『学習』が行われない状態になる。
これが多層で発生する勾配消失問題の原因の一つである。
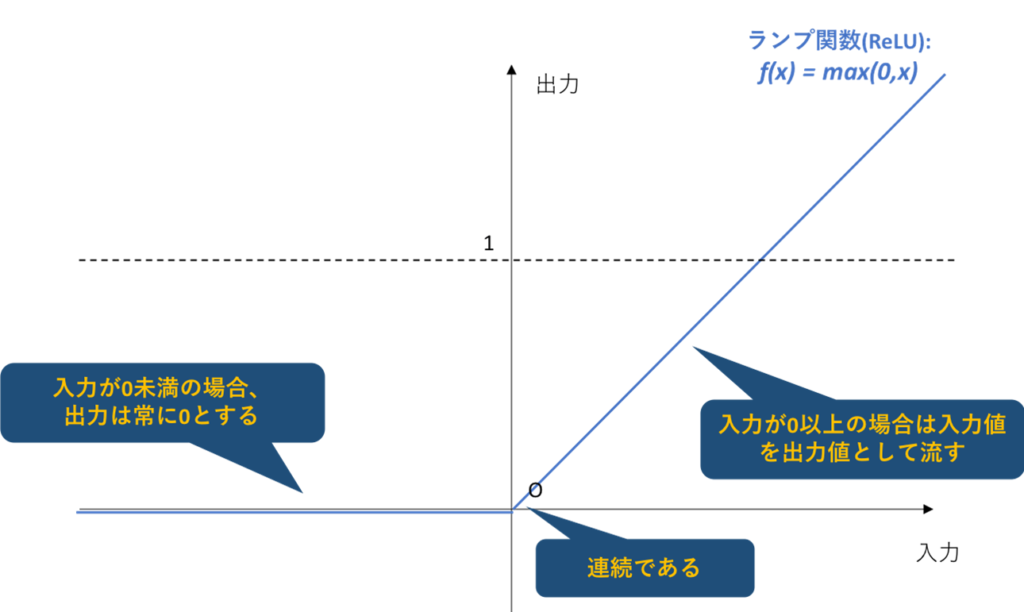
その為、Deep Neural Networkでは非線形活性化関数としてReLU:f(x)=max(0,x)(ランプ関数)が一般的に採用されている。
ReLUは定義域が正のときは恒等写像になり、微分\( f’\left( z\right) =1 \)になる。
1は何回かけても1なので、入力層側への誤差は薄まる事はない。
ReLUは多層化(Deep Neural Network)に向いた活性化関数と言える。
これが勾配消失という問題に有効に働く。
尚、シグモイド関数の微分=導関数が元の関数を使った形になるという便利さがある。
$$ f\left( a\right) =\dfrac {1}{1+\exp \left( -a\right) } \tag { 4-3} \\ $$
$$ \dfrac {df}{da}=f\left( a\right) \cdot \left( 1-f\left( a\right) \right) \\ $$
https://qiita.com/sakigakeman/items/44af9ffde0550e52495e
◆2-1:第2層の入力と出力
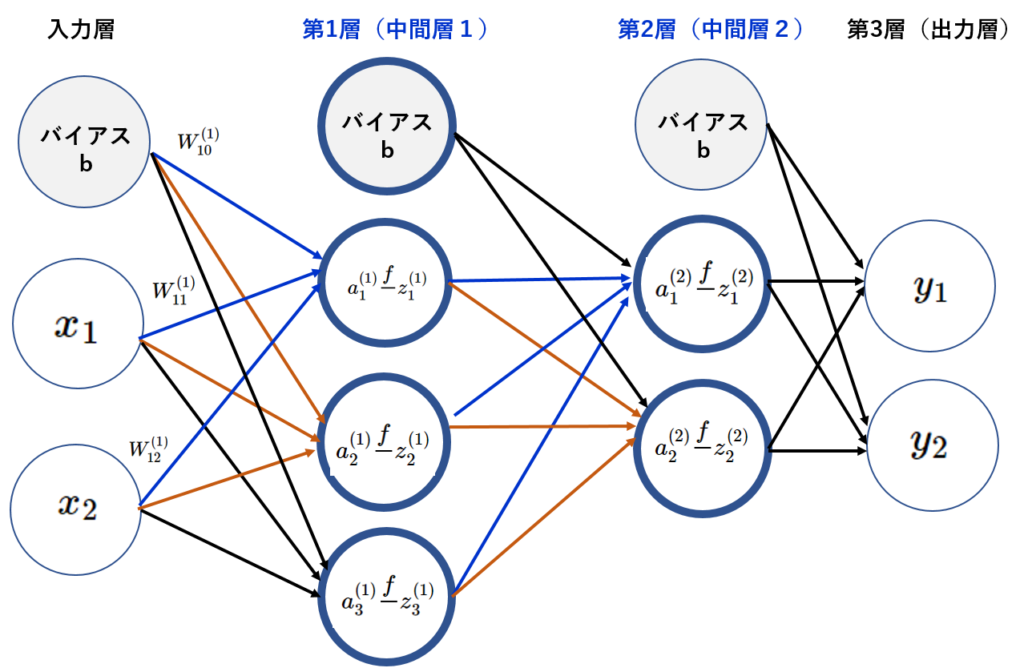
入力情報:\(Z\)←X
$$ Z^ {\left( 1\right) } = \begin{pmatrix} z^{\left( 1\right) }_{1} & z^{\left( 1\right) }_{2} & z^{\left( 1\right) }_{3} \end{pmatrix} = \begin{pmatrix} 0.57444252 & 0.66818777 & 0.75026011 \end{pmatrix} \\ $$
$$ W^{\left( 2\right) }=\begin{pmatrix} W^{\left( 2\right) } _ {11} & W ^ {\left( 2\right) } _{12} \\ W^ {\left( 2\right) } _{21} & W^ {\left( 2\right) } _{22} \\W^ {\left( 2\right) } _{31} & W^ {\left( 2\right) } _{32} \end{pmatrix} =\begin{pmatrix}0.1 & 0.5 \\0. 2 & 0.7 \\ 0.3 & 0.9 \end{pmatrix} \\ $$
$$ A^{\left( 2\right) } =Z^ {\left( 1\right) }W^ {\left( 2\right) } +b^ {\left( 2\right) } \tag { 4-4 } \\ $$
$$ Z^{ \left( 1\right) }W^{\left( 2\right) }=\begin{pmatrix} 0.57444252 & 0.66818777 & 0.75026011 \end{pmatrix}\begin{pmatrix} 0.1 & 0.5 \\ 0.2 & 0.7 \\ 0.3 & 0.9 \end{pmatrix} \\ $$
$$ Z^{ \left( 1\right) }W^{\left( 2\right) }= \begin{pmatrix} 0.416159838 & 1.430186794 \end{pmatrix} \\ $$
\(X\)の列数と\(W\)の行数が一致しないといけない。(行列の積のルール①)
積を取った後の行列サイズに注意。
\(k\)×\(m\)行列と \(m\)×\(n\) の積を取ると\(k\)×\(n\)行列になる。(行列の積のルール②)
$$ b^ {\left( 2\right) } = \begin{pmatrix} W^{\left( 2\right) }_{11} & W^{\left( 2\right) }_{21} \end{pmatrix}= \begin{pmatrix} 0.1 & 0.2 \end{pmatrix} \\ $$
$$ A^{\left( 2\right) } =Z^ {\left( 1\right) }W^ {\left( 2\right) } +b^ {\left( 2\right) } \tag { 4-4 } \\ $$
$$ A^{\left( 2\right) } = \begin{pmatrix} 0.416159838 & 1.430186794 \end{pmatrix} + \begin{pmatrix} 0.1 &0. 2 \end{pmatrix} \\ $$
$$ A^{\left( 2\right) } = \begin{pmatrix} 0.516159838 & 1.630186794\end{pmatrix} \\ $$
◆2-2:第2層からの信号を出力する。
非線形活性化関数(シグモイド関数)の出力値を第2層の出力とする。
$$ f\left( a\right) =\dfrac {1}{1+\exp \left( -a\right) } \tag { 4-3} \\ $$
上記式に
$$ A^{\left( 2\right) } = \begin{pmatrix} 0.516159838 & 1.630186794\end{pmatrix} \\ $$
の値を代入する。
$$ Z^ {\left( 2\right) } = \begin{pmatrix} z^{\left( 2\right) }_{1} & z^{\left( 2\right) }_{2}\end{pmatrix} = \begin{pmatrix} 0.6264937 & 0.83619523\end{pmatrix} \\ $$
◆3-1:第3層の入力と出力
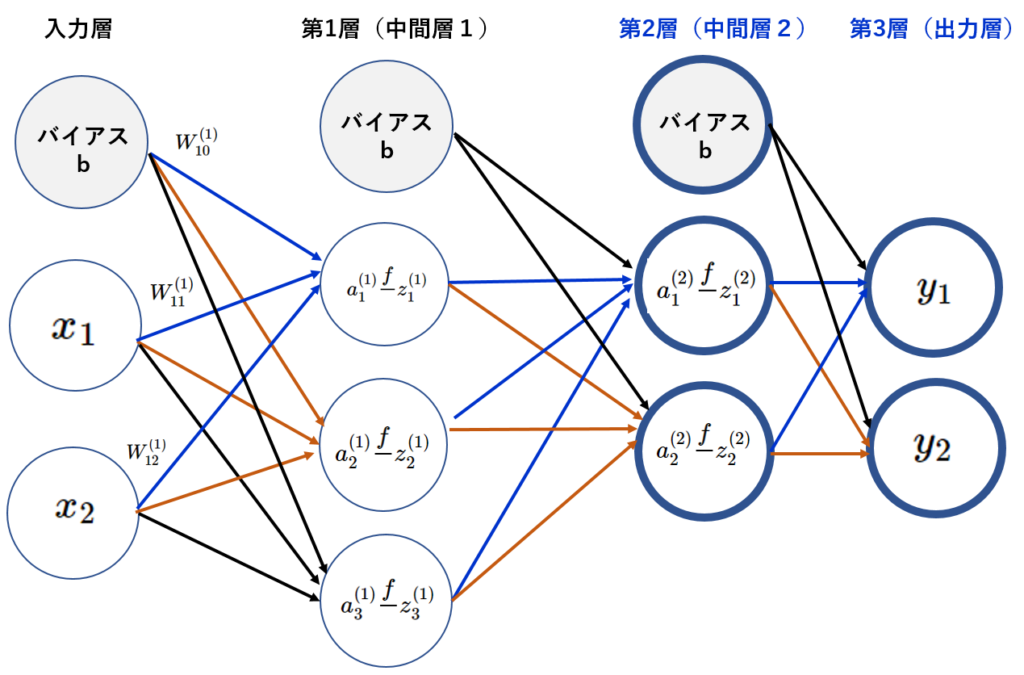
入力設定はこれまでの処理と同じである。
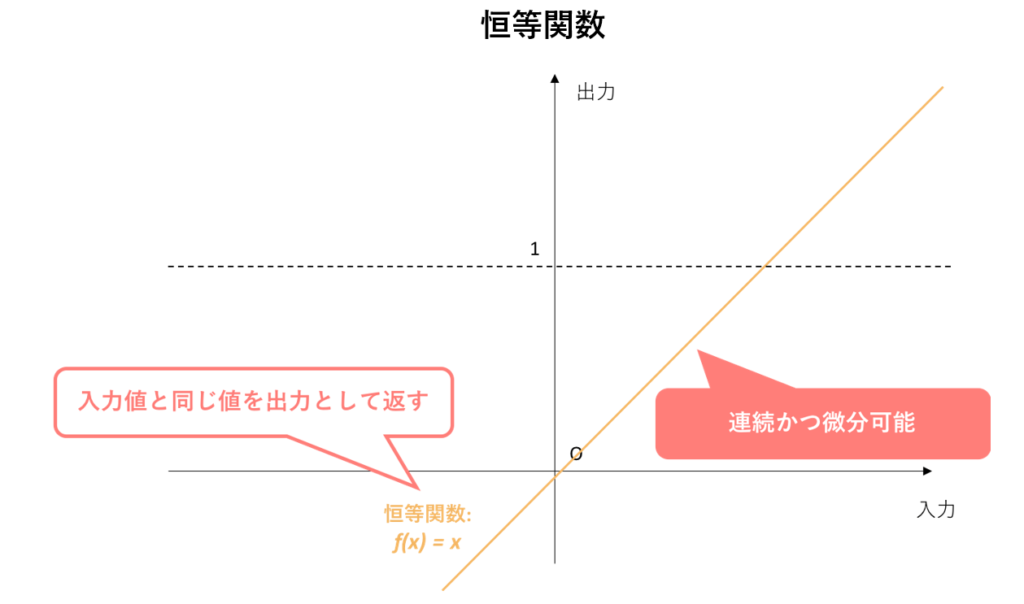
活性化関数として恒等関数を使う。恒等関数は入力をそのまま出力する関数。
入力情報:\(Z\)←X
$$ Z^ {\left( 2\right) } = \begin{pmatrix} z^{\left( 2\right) }_{1} & z^{\left( 2\right) }_{2}\end{pmatrix} = \begin{pmatrix} 0.6264937 & 0.83619523\end{pmatrix} \\ $$
$$ W^{\left( 3\right) }=\begin{pmatrix} W^{\left( 3\right) } _ {11} & W ^ {\left( 3\right) } _{12} \\ W^ {\left( 3\right) } _{21} & W^ {\left( 3\right) } _{22} \end{pmatrix} =\begin{pmatrix}0.1 & 0.3 \\0. 2 & 0.4\end{pmatrix} \\ $$
$$ A^{\left( 3\right) } =Z^ {\left( 2\right) }W^ {\left( 3\right) } +b^ {\left( 2\right) } \tag { 4-5 } \\ $$
$$ Z^{ \left( 2\right) }W^{\left( 3\right) }=\begin{pmatrix} 0.6264937 & 0.83619523 \end{pmatrix}\begin{pmatrix} 0.1 & 0.3 \\0. 2 & 0.4 \end{pmatrix} \\ $$
$$ Z^{ \left( 2\right) }W^{\left( 3\right) }= \begin{pmatrix} 0.229863982 & 0.522352902 \end{pmatrix} \\ $$
$$ b^ {\left( 3\right) } = \begin{pmatrix} W^{\left( 3\right) }_{11} & W^{\left( 2\right) }_{21} \end{pmatrix}= \begin{pmatrix} 0.1 & 0.2 \end{pmatrix} \\ $$
$$ A^{\left( 3\right) } =Z^ {\left( 2\right) }W^ {\left( 3\right) } +b^ {\left( 2\right) } \tag { 4-5 } \\ $$
$$ A^{\left( 3\right) } = \begin{pmatrix} 0.229863982 & 0.522352902 \end{pmatrix} + \begin{pmatrix} 0.1 &0. 2 \end{pmatrix} \\ $$
$$ A^{\left( 3\right) } = \begin{pmatrix} 0.32986398 &0.72235290 \end{pmatrix} \\ $$
https://qiita.com/sakigakeman/items/44af9ffde0550e52495e
恒等関数:\(y\)=\(x\)
受け取ったののままの値を変換せずに出力する。
$$ A^{\left( 3\right) } = Y \\ $$
出力層
$$ Y= \begin{pmatrix} y^{ \left( 1\right) } & y^{\left( 2\right) } \end{pmatrix} = \begin{pmatrix} 0.32986398 &0.72235290 \end{pmatrix} \\ $$
これで第三ステップの準備は出来た。
■■第三ステップ: 深い階層のDNN (Deep Neural Network ) を学ぶ■■