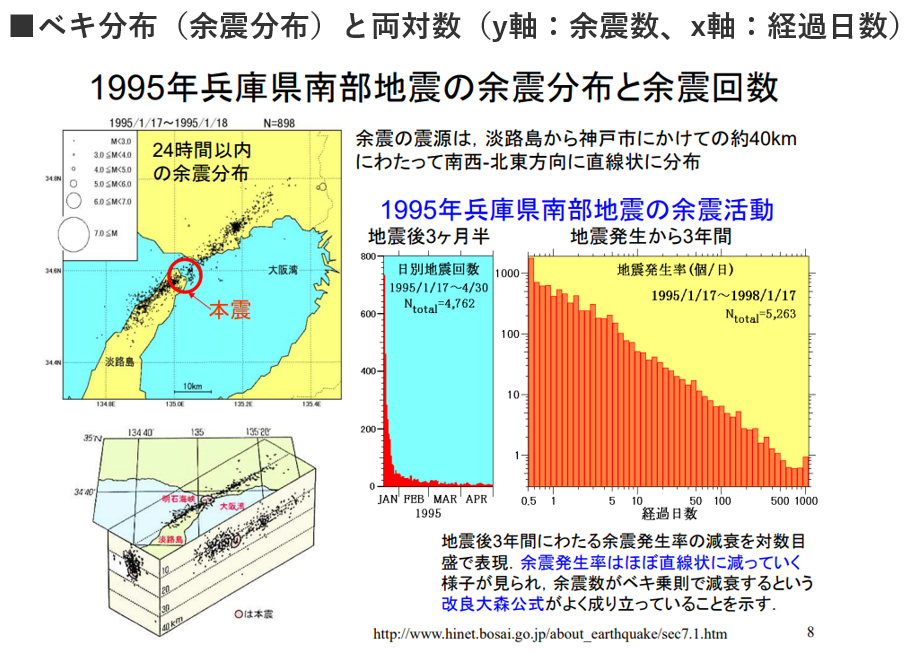
■ベキ分布と正規分布
・株価は対数正規分布(将来のある時点での株価)に従うかか?それともベキ分布(ブラック・スワンの出現)に従うか?の問いが
⇒リーマンショックの際に大いに議論された記憶がある。
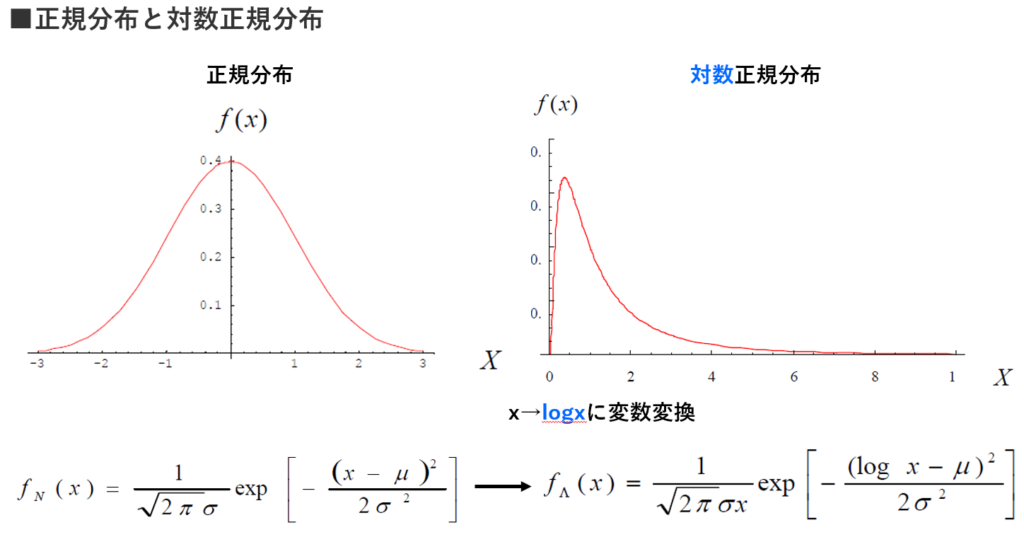
出典:対数正規分布 中央大学 香取研究室 浅野 翔 金田 佐和子
・金融工学の花であった『ブラック・ショルズ方程式』は
⇒金融商品の原資産価格変動は「ランダムウォークに従う(将来のある時点での価格分布は対数正規分布に従う)」との仮定で金融取引が実践されてきた。
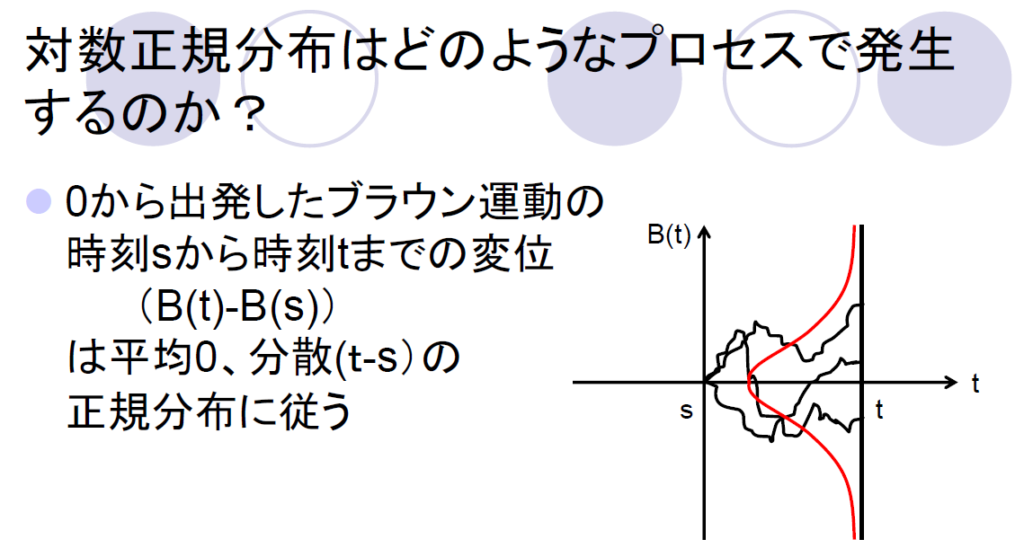
出典:対数正規分布への入門 中央大学 香取研M1 和泉南
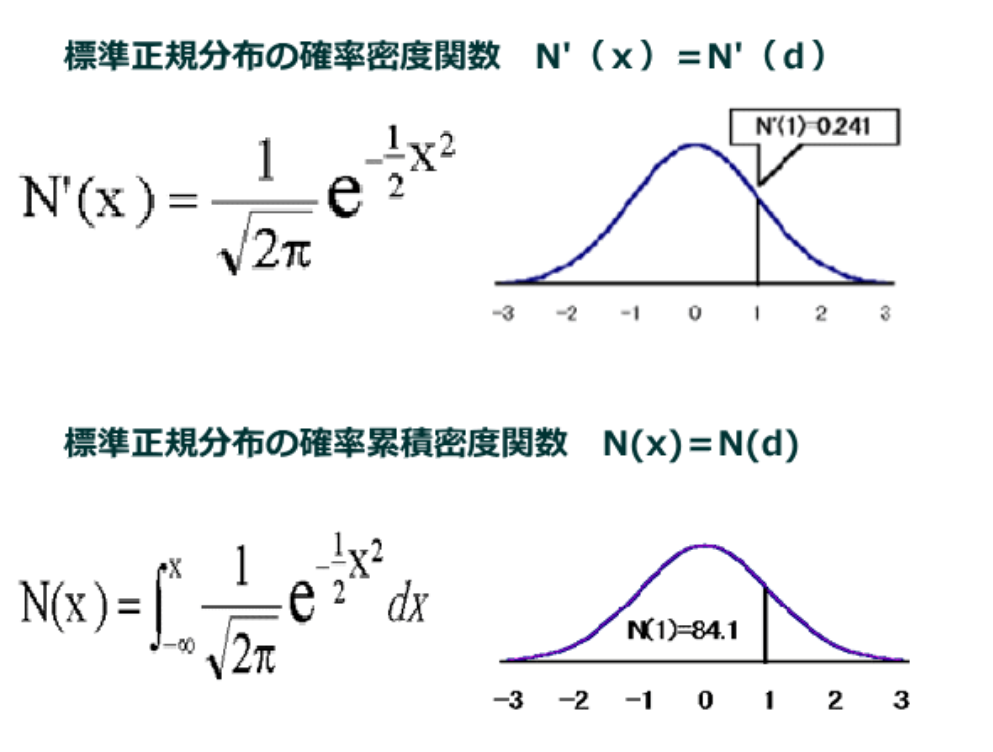
■汎用ブラック・ショルズ・モデル(通貨・先物・債券等のオプション価格計算式)

・N(d):標準正規分布の確率累積密度関数、N’(d):標準正規分布の確率密度関数
⇒N(d)という関数を微分するとN’(d)という関数になり、逆に、N’(x)という関数を積分するとN(x)になる。
注)\(e^{-a}\)と指数にマイナスがついているものは、\(e^{a}\)の逆数で\(\frac{1}{e^{a}}\)であることを示す。
\(e^{-a}=\frac{1}{e^{a}}\)
◆対数計算の復習
・ある数 aをp乗してbになるとした場合、即ちb= ap となる場合の、べき指数p のことを指す。
⇒このp を「 aを底(てい)とする b の対数」と呼ぶ。
⇒このpが loga bと表現され、
⇒aは「底(てい)」
⇒b は「真数」と呼ばれる。
即ち、以下の関係となる
\(p=\log ab\) ⇔ \(b=a^{p}\)
a(底)をp(対数)乗ずるとb(真数)になる。

また、一般的な変数xに対応する対数を与える関数を『対数関数』と呼び、
通常\(\log_{a}x\)と表されるが、以下の関係となる。
\(\log_{a}x\) ⇔ \(x=a^{y}\)
・常用対数
10を底とするものを「常用対数」と呼び、記号「\(\log _{10}x\)」で表現される。
・自然対数
底をe(ネピアの数(すう))にしたものを自然対数という。e=2.71828…で、loge または、ln という記号を使う。
「 x=loge株価」では、xという株価の対数が正規分布することを意味している。
出典:https://www.findai.com/kouza/4009opt.html
・対数の基本公式
⇒「掛け算が足し算に、割り算が引き算に、n乗がn倍に、n乗根が1/n倍に」なることから、特に大きな数を扱う場合の計算が楽になることになる。
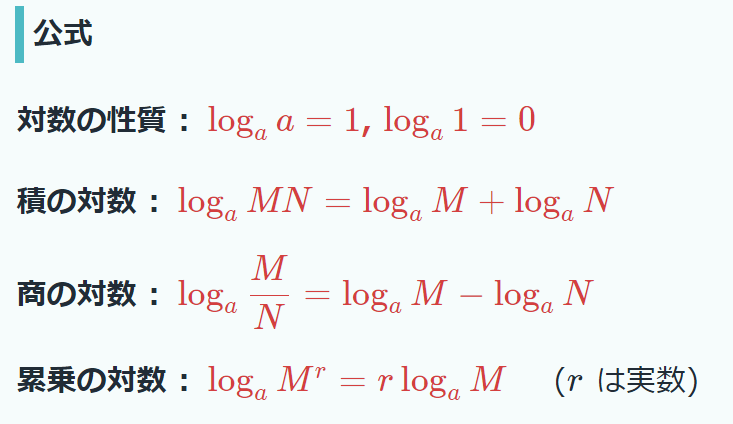
◆忘れた頃に時々訪れる『大暴落=大変動』事例としてのリーマンショック
⇒資産価格(株価等)の暴落の発生頻度は『べき分布に従う』が観察される。
⇒金融工学界からつまはじきされたベノワ・B・マンデルブロ博士が
⇒過去の綿花の価格変動推移から
⇒暴落発生頻度は
⇒ベキ分布に従うを提唱した事が思い出される。
■ベキ分布が観測される現象
・有名なのは地震のマグニチュードの大きさと頻度の関係(グーテンベルグ・リヒター則)
⇒火山噴火、雪崩等の自然災害の規模と頻度の関係
・ベキ関数とは
⇒現象の2つの観測値(規模と頻度)が、ベキ乗で比例するという関係
⇒\(y=x^{-b}\)
⇒\(x\)現象の規模(サイズ)
⇒\(y\)現象の頻度(数)
⇒\(b\)をマイナスにしたのは、「規模」が大きなものは「頻度」が少なる関係(反比例)を表す為に。
出典:https://takun-physics.net/4615/
・指数関数
⇒\(y=e^{-x}\)
⇒\(x\)(規模)が指数となっており、
⇒底がネピアの数\(e\)となっている。
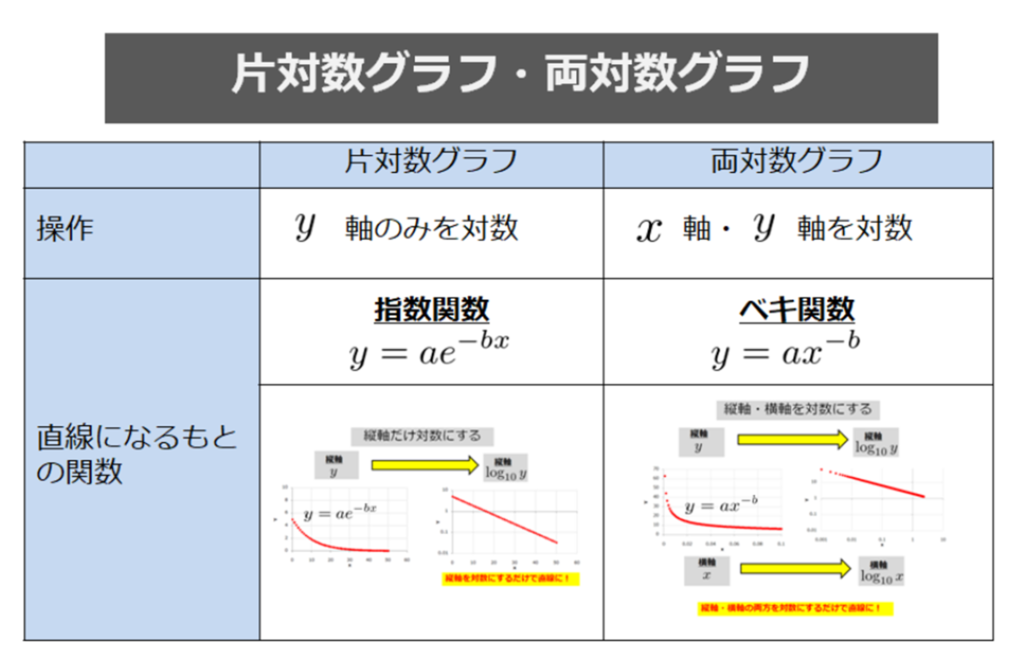
◆ベキ分布の数式
\(y=ax^{-b}\)
・両辺で対数(\(\log\))を取る(\(x\)軸、\(y\)軸を対数)
⇒\(\log _{10}y=\log _{10}\left( ax^{-b}\right)\)
⇒\(\log _{10}y=\log _{10}a+\log _{10}x^{-b}\)
⇒\(\log _{10}y=log _{10}a-b\log _{10}x\)
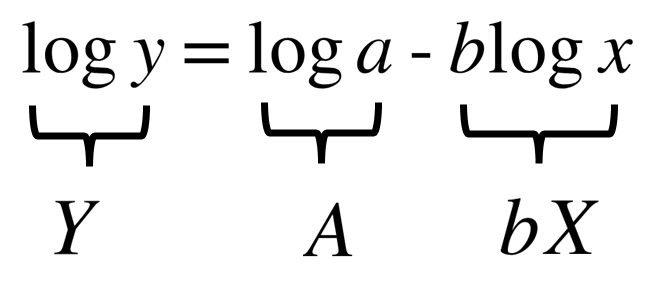
とおくと

となり、\(x\)軸、\(y\)軸共に対数の場合に一次式(線形)になる。

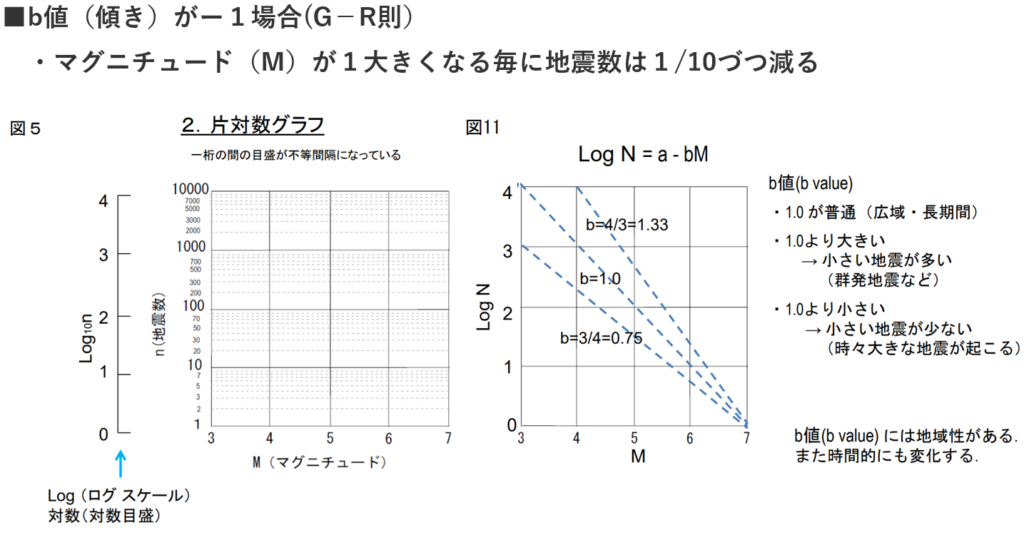
■グーテンベルグ・リヒター則(G-R則)
・地震の規模(\(x\))と発生頻度(\(y\))の間に見られる経験則
⇒小さい地震は多数発生するが、大被害が生じるような大きな地震は稀にしか発生しない。
・「マグニチュード」と『その発生個数の対数』との間には直線的な関係(直線で近似出来る)が成り立つ。
\(\log n\left( M\right) =a-bM\)
の式で表される。
⇒Mはマグニチュード、n(M)はマグニチュードMの地震の発生個数、
⇒N(M)はマグニチュードM以上の地震の総数(積算地震数)
⇒aとbは定数で
⇒bは直線の傾きを表しており、
⇒地下の応力状態を表す重要なパラメータの一つであると考えられている。
⇒尚、bは地域性などに違いがあり、
⇒bが大きいほど相対的に小さな地震が多くなる。
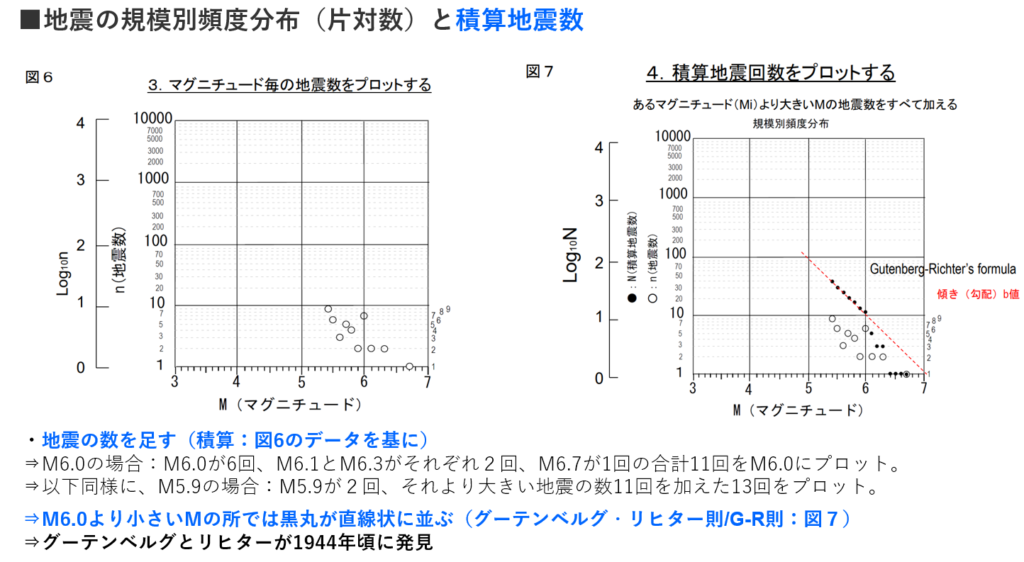
出典:http://namazunokai.starfree.jp/pdf/lecture_03.pdf 地震の規模別頻度分布 梅田 康弘 京大名誉教授
出典:https://slidesplayer.net/slide/11572045/ 首都圏および東葛地域の地震について 瀬野徹三(東京大学地震研究所) 2012.09.29布施新町二自協ふれあいセミナー
・マグニチュードの設定範囲(マグニチュード別頻度分布)
⇒マグニチュードがある程度小さくなると頻度が頭打ちになり、
⇒G-R則からはずれる部分が必ずある。
⇒G-R則に当てはめる際には用いる地震データがポイントになる。
・マグニチュード別頻度分布において
⇒直線性の良いマグニチュード範囲に対して当てはめる必要がある。
⇒G-R則を当てはめる際にマグニチュードの下限と上限の設定がある。
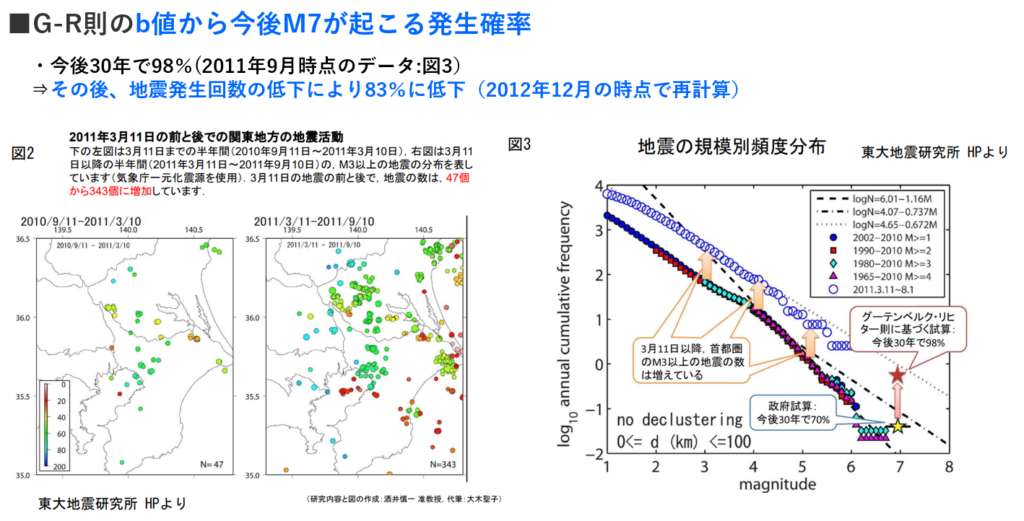
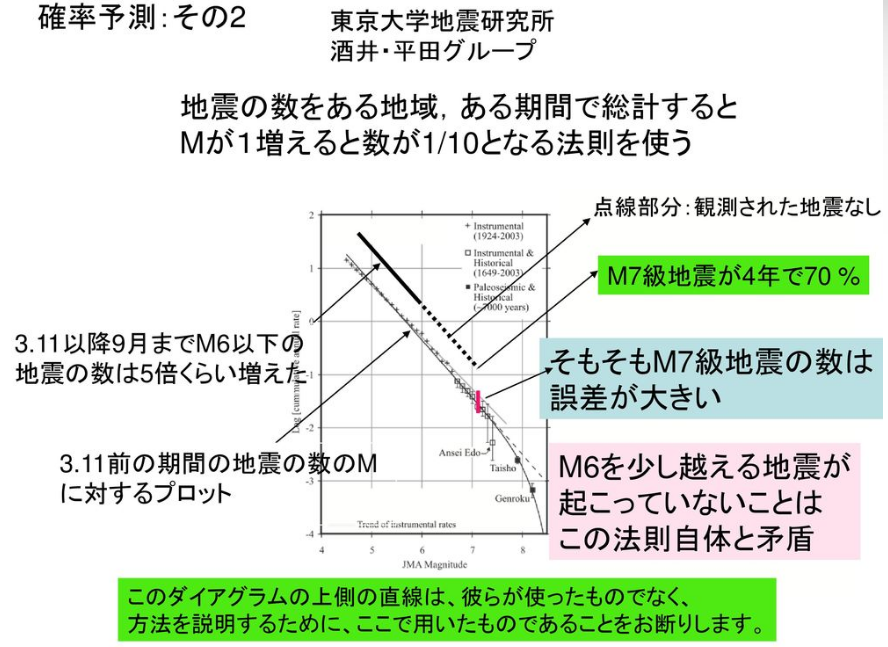
注:地震の発生確率について詳細な内容はhttp://namazunokai.starfree.jp/pdf/lecture_04.pdf&_05.pdfご確認願います
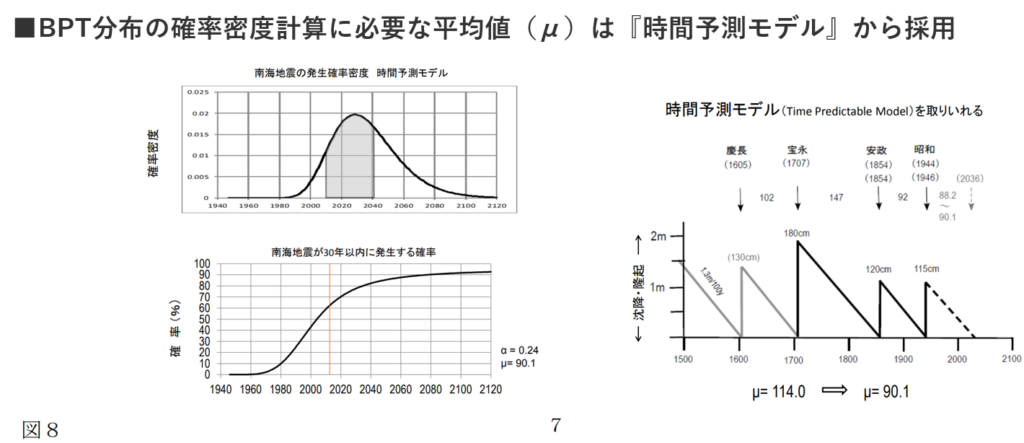
同資料にて発生確率の計算としてBPT分布(Brownian Passage Timeの略)が採用され、情報更新過程も組み込まれており、その計算結果をG-R則で検証されている。
出典:http://namazunokai.starfree.jp/pdf/lecture_04.pdf&_05.pdf
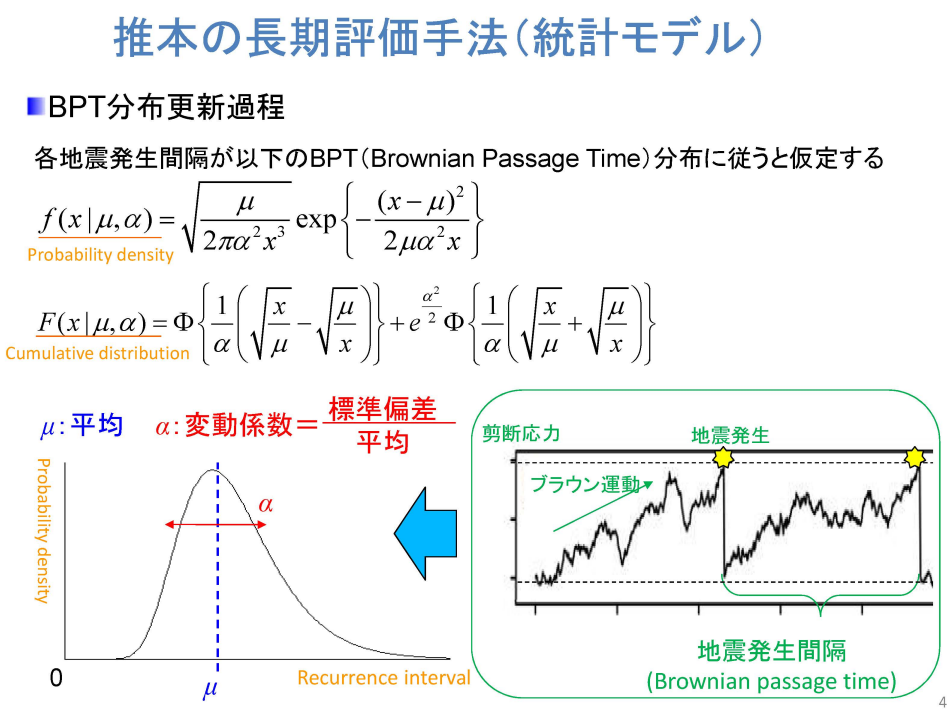
出典:https://www.yonden.co.jp/assets/pdf/energy/atom/safety/sshac_project/workshop_2/ws2-2-03.pdf ベイズ統計モデルを用いた活断層の長期予測 東京工業大学 野村 俊一
・BPT分布の確率密度関数(f)の式
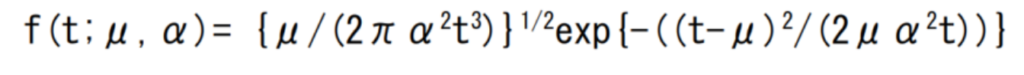
注:\(\sqrt{a}=a^\frac{1}{2}\)
\(\sqrt{\frac{u}{2\pi a^{2}x^{3}}}=\left({\frac{u}{2\pi a^{2}x^{3}}}\right)^\frac{1}{2}\)
⇒BPT分布(確率密度関数:Probability density)の式をエクセルに入力(図6の表のC列の7行目(経過年数2年目)の入力/μ:114、σ:0.24)
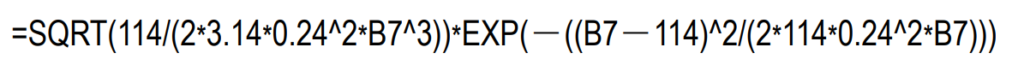
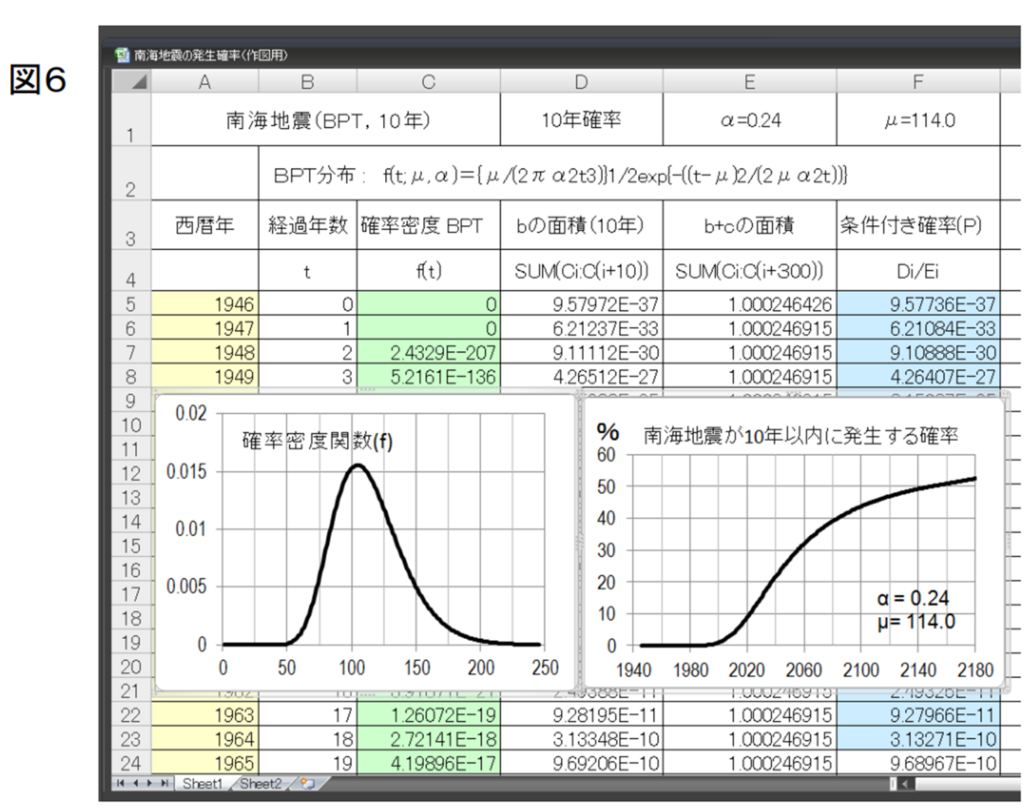
出典:http://namazunokai.starfree.jp/pdf/lecture_04.pdf
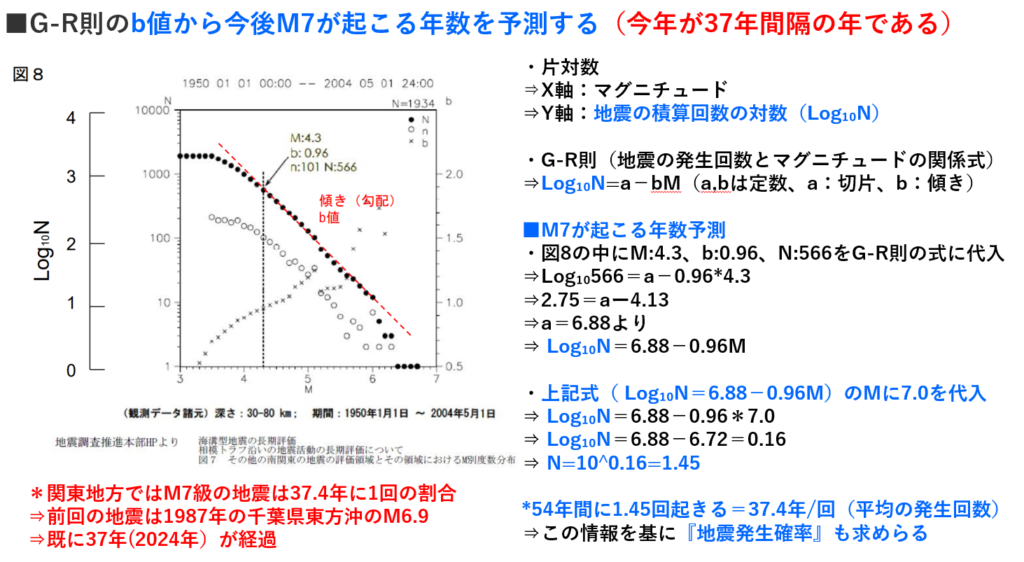
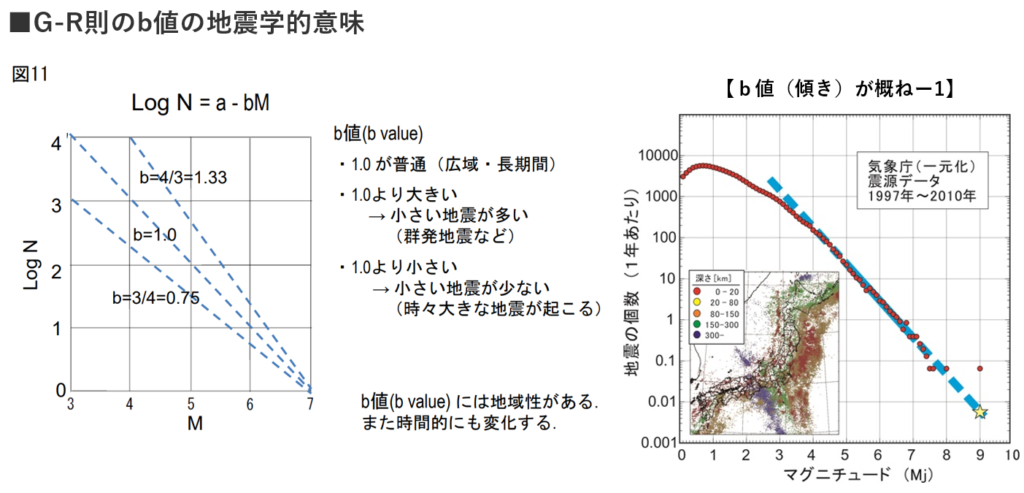
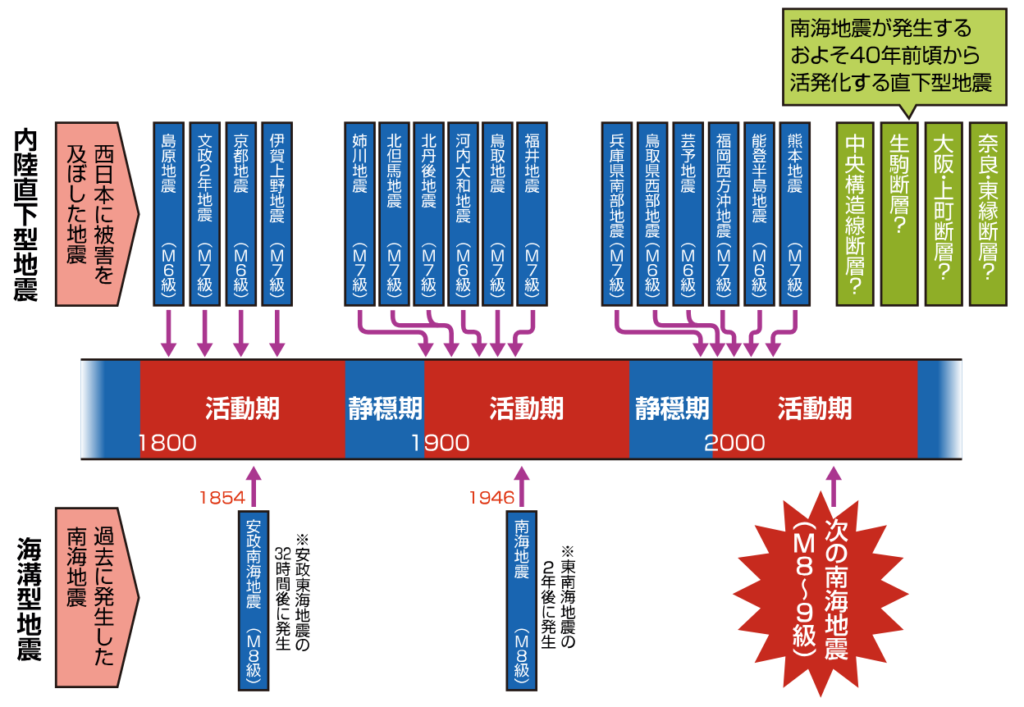
■マグニチュードと地震の数の関係式(G-R則:Log₁₀N=aーbM)から東日本大震災(M9.0)に直面して
・b値はだいたい0.9~1くらいの値になる。
⇒b値が1の時(G-R則:Log₁₀N=aーbM)
⇒マグニチュードが1大きくなる毎に
⇒地震の数は1/10に減少する。
⇒\(10^{-1}=\frac{1}{10^{1}}=0.1\)、\(10^{-2}=\frac{1}{10^{2}}=0.01\)、\(10^{-3}=\frac{1}{10^{3}}=0.001\)・・・
出典:http://namazunokai.starfree.jp/pdf/lecture_03.pdf
・マグニチュード5(M5)の地震を1,000回(10^3)起きるとすると
⇒M6の地震は100回(10^2)、M7の地震は10回(10^1)、M8の地震は1回(10^0)起こることになる。
・マグニチュード5(M5)の地震を10,000回(10^4)起きるとすると
⇒M6の地震は1,00回(10^3)、M7の地震は100回(10^2)、M8の地震は10回(10^1)、M9の地震は1回(10^0)起こることになる。
・M9級地震は869年貞観地震、2011年3月11日東日本大地震の2回だけ(南海トラフ3連動はM9想定)
⇒下記右図の予測式(G-R則)の直線を下方に引き延ばすと
⇒1年当りの地震数は0.066個になる
⇒15年(1/0.066≒15)で1回の割合でM9級の地震が発生する事になる。
⇒M7級やM8級とは違う評価軸(G-R則以外の?)の検討に直面した。
出典:左図)地震の規模別頻度分布 梅田 康弘 京大名誉教授 右図)東京大学大学院情報学環 総合防災情報研究センター 防災コラム 古村 孝志(2012年12月1日)
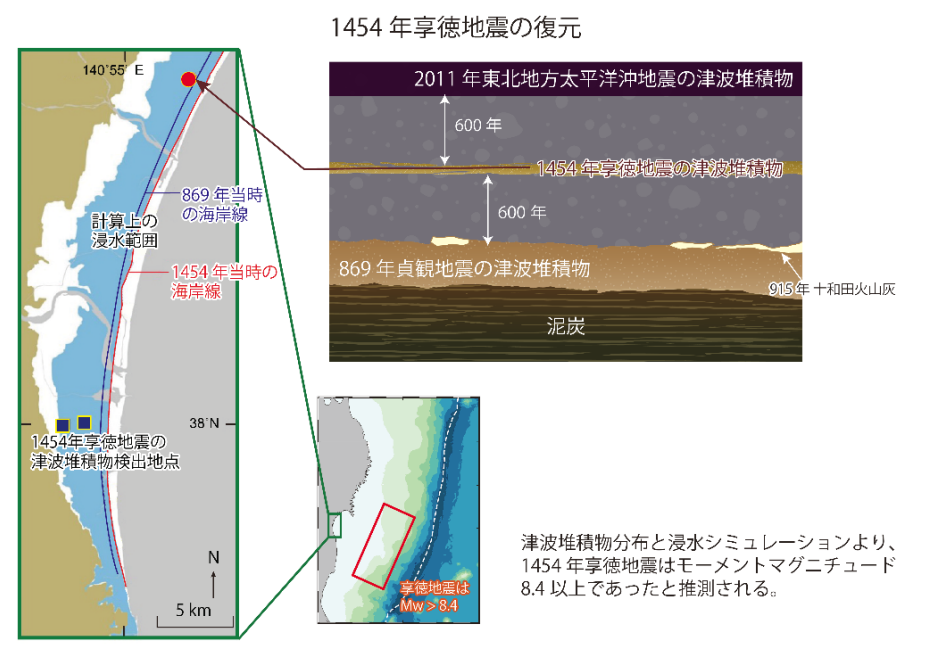
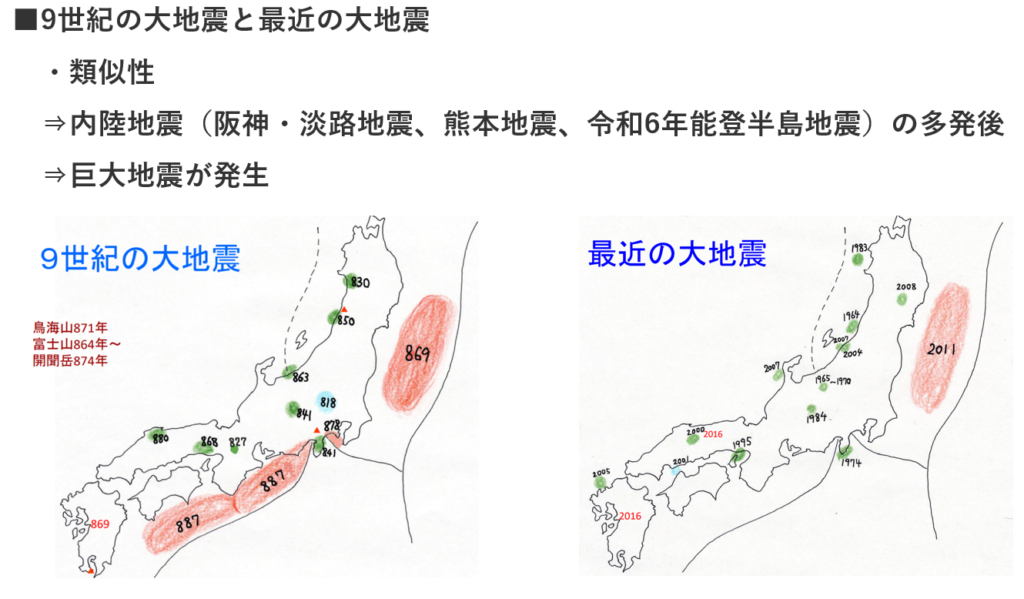
■津波堆積物等の地質学的情報と古文書情報の新たな視点の提供
・M9級の3.11は貞観地震(869年)以来の地震であったのか?
⇒地道な津波堆積物調査から
⇒過去3,000年間で4回の巨大津波による津波堆積物が宮城県から福島県にかけての太平洋沿岸で見つかっている。
⇒1回は、864年の貞観地震によるもが確認されている。
⇒もう1回は次のいずれか。1455年の享徳地震(M8.4以上、室町時代:歴史的記録が少ない)、1611年慶長三陸地震(M8.4以上、伊達政宗が仙台藩を統治していた時代)。
尚、貞観地震に匹敵する巨大地震が室町時代(享徳地震)にも発生していた可能性が高いことが、東北沖地震の前年に指摘されていた。
⇒他の2回は(4世紀、紀元前4~3世紀)
⇒下図の600年サイクルも浮かび上がる。
出典:https://www.eri.u-tokyo.ac.jp/YOTIKYO/OpenReport/H30/H30SeikaGaiyo.pdf 「災害の軽減に貢献するための地震火山観測研究計画」平成30年度年次報告 科学技術・学術審議会測地学分科会 地震火山部会

出典:「新菱沼津波堆積物地層」提供/岩沼市教育委員会
注:宮城県岩沼市教育委員会の調査によって発見された津波堆積物のある地層。いちばん上の白っぽい第1層は東北沖地震で堆積した。第4層と第8層も津波堆積物の可能性がある。放射性炭素年代測定などの結果から、第4層の年代は16〜17世紀ごろ、第8層は8〜9世紀ごろと推定している。
【追加情報(2024年3月17日):600年サイクル説に関連する情報】
「そろそろ満期だ」M9クラスが約300年に1回発生“千島海溝巨大地震”の怖さ 震度3でも津波10m超のケースも(tbc 東北放送)
https://news.yahoo.co.jp/articles/709dd493745c27338acc82702841770720a4d12b?page=1
今後、高い確率で発生が予想される巨大地震に、北海道沖を震源とする千島海溝地震があります。宮城でも10メートル以上の津波が予想されていて、専門家の観測で、それを裏付けるプレートの動きも見えてきました。
■巨大地震「千島海溝モデル」とは
北海道沖の千島海溝沿いや三陸沖の日本海溝沿いでマグニチュード7以上の地震が起きた場合に、その後、発生する可能性があるマグニチュード9クラスの巨大地震への注意を促す情報です。
・この巨大地震による宮城県の被害想定は、「日本海溝モデル」が震度6強で津波の高さは16メートル、津波による死者は8500人。
・一方、「千島海溝モデル」は、震源が遠いため震度は3以下ですが、津波の高さは11メートルで、震災後に整備された防潮堤を越える計算です。死者は5200人にのぼります。
・場合によっては、前震にあたる地震が無く、
⇒注意情報が出されずに
⇒いきなり北海道沖の千島海溝沿いや三陸沖の日本海溝沿いでマグニチュード9クラスの巨大地震が起こるケースもあります。
■1611年の『慶長三陸地震』での大津波とは
・慶長16年、1611年に宮城を襲った慶長三陸地震。大津波により仙台藩で1783人の犠牲者が出ました。
岩沼市の沿岸部では、この慶長津波と、869年の貞観津波、そして、13年前の東日本大震災という3つの津波の痕跡を示す地層が2013年に見つかりました。現在、この地層は市の図書館に保存されています。
ところで、この慶長三陸地震については、震源は三陸沖と推定されてきました。
■慶長三陸地震の震源は千島海溝だった可能性が
・産業技術総合研究所の岡村行信さんは、「実は千島海溝が震源だった可能性がある」と考えています。
⇒「ほぼ同じ時期に北海道の東部、十勝から根室沿岸に巨大津波が発生したということが分かっています」
⇒これは、北海道東部の浜中町で見つかった地層です。17世紀前半に津波が押し寄せたことを示す砂の層がみられます。
⇒岡村さんは、この津波はかなり内陸まで届いたとみられることから、震源は千島海溝付近で、これが慶長地震として宮城にも津波をもたらしたとみています。
⇒「(北海道東部の)当時の海岸から3キロ4キロ内陸側まで砂が運ばれていったと、そういう砂の層の分布が見つかっているわけですね。
⇒慶長三陸津波は、北海道道東付近(千島海溝)の巨大地震によって発生した可能性があると考えています」
■千島海溝で進む地殻変動
いま、千島海溝では次の巨大地震に向けた地殻変動が進んでいます。
東北大学災害科学国際研究所 木戸元之教授: 「過去の履歴を見るとM9クラスが三百何十年に1回は起きている、そろそろ”満期”なので、次に起こるのはそのクラスである可能性が割とある」
木戸元之教授ら東北大学などのグループは、千島海溝周辺のプレートの動きを調べる観測を2019年から行っています。ウェーブグライダーと呼ばれる無人で動く船などを使って、海底に沈めた装置が発する音波をとらえるものです。
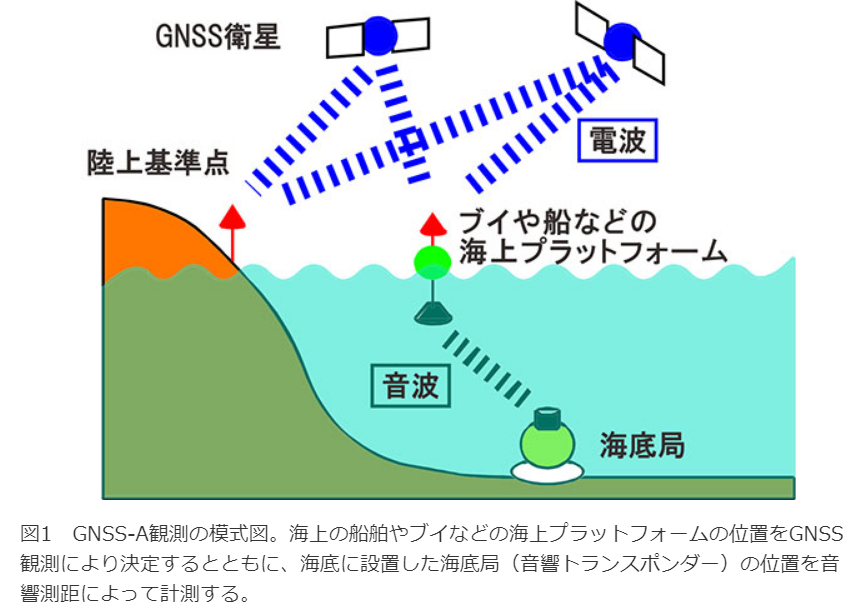
出典:https://www.jamstec.go.jp/j/about/press_release/20200930/ 海洋研究開発機構
海底の観測装置は、千島海溝の南東側から沈み込む太平洋プレート上に1か所、それに固着して引きずられる北西側の陸側のプレート上に2か所設けられています。
・実際観測した結果、
⇒この沈み込む(太平洋)プレートとほぼ同等な速度で(陸側のプレートの)この21という点と22という点が動いていることが分かりました。
⇒観測の結果、陸側のプレートが広い範囲で太平洋プレートと同じように動いているため、
⇒両者が大規模に固着している可能性が高いことが分かったのです。
⇒海溝の最深部である海溝軸に近い所まで固着していると、
⇒これが一気に滑った際には巨大な津波を引き起こすと言います。
「実際に2011年の東北沖地震の時がまさにそれで、海溝軸まで完全に滑って、そのせいで非常に大きな津波が発生した。
それと同じようなことが、もしここまで固着して、ひずみがエネルギーをためていると起こりうる」
出典:https://news.yahoo.co.jp/articles/0c80f954b9479bfcdb599d98b31d94b9d7de18d0?page=1
■千島海溝巨大地震への備えは…
千島海溝巨大地震は今後30年以内の発生確率が7から40%とされ、国は「切迫性が高い」と評価しています。宮城では揺れが小さくても大きな津波をもたらすという特徴を理解し、備えることが求められます。
・千島海溝や日本海溝でマグニチュード7以上の地震が起きて注意情報が出された場合、
⇒その後1週間以内にマグニチュード9クラスの巨大地震が起きる確率は100回に1回程度とされています。
⇒ただ、それでも普段よりは大幅に高まるということを理解しておく必要があります。
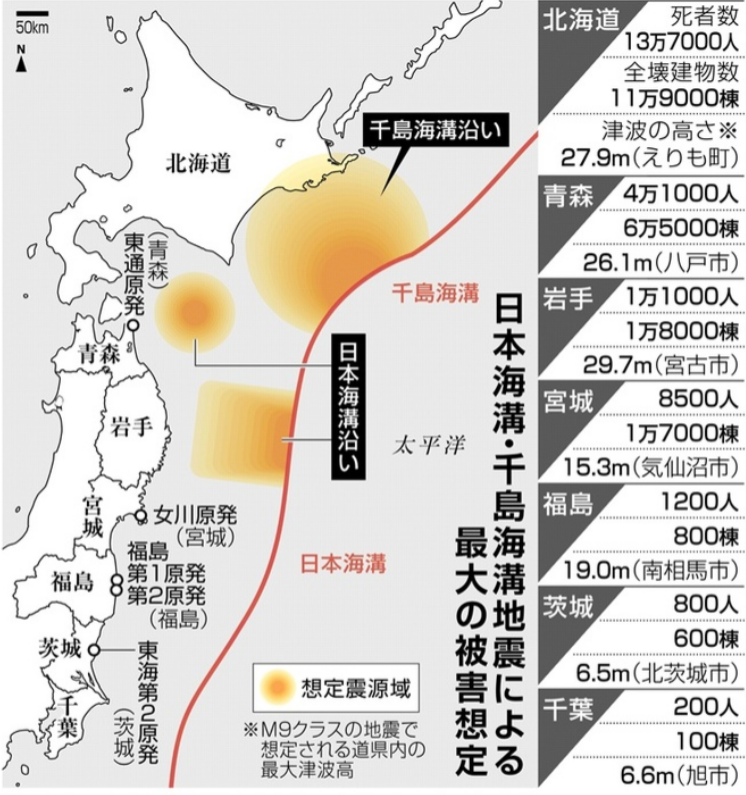
出典:https://www.nishinippon.co.jp/image/424092/ 西日本新聞 M9で死者19万9000人想定 日本海溝・千島海溝地震 津波早期避難なら8割減 (2021年12月22日)
出典:http://ares.tu.chiba-u.jp/marulab/note/bosai/Lec4.pdf 防 災 工 学 第4回 千葉大学 工学部 都市環境システムコース 丸山 喜久
■マグニチュードと地震のエネルギーの関係
◆令和6年能登半島地震で痛感した事
・震度で判断すると
⇒「点」で評価することに繋がり、局所的な被害を想起することになる。
⇒巨大地震に直面した際、『面』で判断しなと
⇒全容把握を想像する事が困難になり、当然事前対策も疎かになることを思い知らされた。
・『面』で地震被害を想定した場合
⇒『マグニチュード(地震のエネルギーE)』が評価軸になり、
⇒地震のエネルギーEの『大きさ比較』になる。
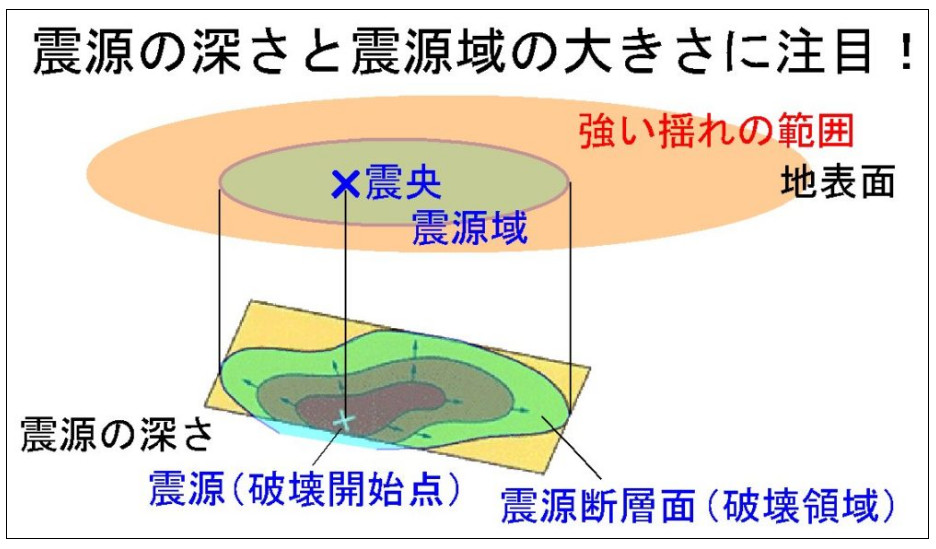
出典:https://mtl-muse.com/study/earthquake/sourcefault/ 大鹿村中央構造線博物館
・全容が掴めないとよく言われる令和6年能登半島地震(Mj:7.6)
⇒平成7年阪神・淡路地震(Mj:7.3)との地震エネルギーEで比較をすれば
⇒災害規模が極めて大きい(E:2.8倍大きい)事が想像出来る。
※気象庁マグニチュード:Mj、モーメントマグニチュード:Mw(世界標準指標)
⇒地震発生後の初動対応で自衛隊の逐次投入が適正であったかが問われるが
⇒余震が頻発する中で現地にいち早く駆けつけ、
⇒建物崩落の危険性と隣り合わせの中で建物に取り残された住民の救援活動をしている
⇒各県の消防隊の即時救援活動には頭が下がる。
・防災計画の情報更新を怠っていたこと(=地方自治体行政の質の劣化)が今回の震災で判明
⇒質の低い『首長』を選挙で当選させ続けていると
⇒大規模災害に直面した際、古臭い防災計画で対応せざるを得ない行政により
⇒選挙民は二次的な被害(孤立集落等)を強いられている姿をニュースを介して目当たりにした。
⇒事前の行動計画(例:地域生活継続計画)の質の低さを露呈しており、『減災』どころか逆に『人災』事例でもある。
尚、支援金箱に僅かな金額を寄付したが
⇒石川県の今年度予算案として大阪万博予算に¥1,000万円が計上された理由が
⇒大阪維新の関係者と知り合いである為と公言した現知事のニュースを知り
⇒2度と個人としては支援金箱に寄付はしない。
復興(防災整備を含む)にお金をつぎ込む事を優先しない
石川県の行政に対して
個人が自主的にする支援金をためさせられる。
一方、三重県では事前に道路寸断等による
孤立集落対策として
既に防災ヘリポート等も整備しつつあるとの
ニュースを知る。
⇒首長の選出は真剣に能力を見極めて投票しないと自ら被害を被る事になると大いに痛感した。
尚、自衛隊の大型ヘリによる救援活動の際、着陸に適した場所(接地面の強度等の色々な条件に適う)を見つける事も苦労したとのニュースを今回の地震で初めて知った。
◆『地域住民による』減災に繋がる避難計画と避難訓練事例(日常生活継続計画の一例:まずは生命)
・5分で避難、全員無事 「奇跡じゃなく訓練」 津波襲来の高齢地区・珠洲市
⇒約40世帯90人ほどが暮らす町北部の寺家下出地区も地震から間もなく津波に襲われ、多くの住宅が倒壊。
⇒それでも大半を高齢者が占める住民は5分以内に高台に避難して全員無事だった。
⇒「この地震なら津波が来る」。
⇒東日本大震災以降、大地震と津波を想定した避難訓練を年1、2回続けてきた住民は、
⇒揺れが収まると荷物を持たずに、体一つで坂道などを上り、高台の集会所に向かった。
・近所同士で声を掛け合い、足の悪い人を背負うなど協力。
⇒地震から5分ほどで全員が集会所に到着すると、津波が到達したという。
詳細内容は以下RLのJIJI.COM記事(1/16(火) 7:07配信)
https://news.yahoo.co.jp/articles/9e863ea073b33b933af5d2e68d8597c679abf182
地域に住んでいるリーダーと住民のスマートさが際立つ事例である。
各県から素早く救援に来ている消防隊の貴重なリソースの有効な活用に繋がる。
■地震のエネルギーをE、マグニチュードをMとすると、次式が成立する
\(\log _{10}E=4.8+1.5M\)
・直下型令和6年能登半島地震対平成7年阪神・淡路地震の地震エネルギー比較
⇒1995年1月17日:Mj=7.3のエネルギーをE₁(深さ16km、最大震度7)
⇒2024年1月1日:Mj=7.6のエネルギーをE₂(深さ16km、最大震度7)
\(\log_{10}E_{2}=4.8+1.5\times 7.6=16.2\)
\(\log_{10}E_{1}=4.8+1.5\times 7.3=15.75\)
商の対数の公式より
\(\log_{10}E_{2}-\log_{10}E_{1}=\log_{10}\begin{aligned}E_{2}\\ \overline{E_{1}}\end{aligned}\)
従って
\(=\log_{10}\begin{aligned}E_{2}\\ \overline{E_{1}}\end{aligned}=0.45\)
\(\dfrac{E_{2}}{E_{1}}=10^{0.45}=2.81\)
・令和6年能登半島地震の地震エネルギーは
⇒平成7年阪神・淡路地震の
⇒2.8倍


出典:https://weathernews.jp/s/topics/202304/060275/ ウェザーニュース
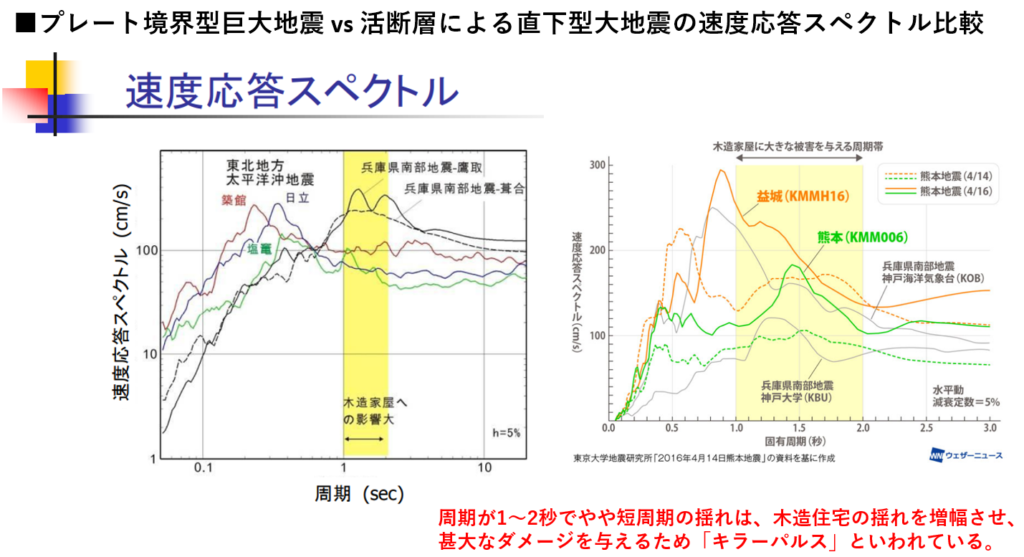
出典:左図)https://www.mhlw.go.jp/topics/bukyoku/kenkou/suido/tantousya/dl/s01.pdf 東日本大震災地震動の特徴と被害との関係 金沢大学理工研究域環境デザイン学系 宮島 昌克
<参考比較>
・令和5年能登半島 群発地震(2023年5月5日:M=6.5(深さ12km、最大震度6強)
・令和6年能登半島地震(2024年1月1日):M=7.6(深さ16km、最大震度7)
・直下型令和6年能登半島地震対令和5年能登半島 群発地震エネルギー比較
⇒2023年5月5日:Mj=6.5のエネルギーをE₁(深さ12km、最大震度6強)
⇒2024年1月1日:Mj=7.6のエネルギーをE₂(深さ16km、最大震度7)
\(\log_{10}E_{2}=4.8+1.5\times 7.6=16.2\)
\(\log_{10}E_{1}=4.8+1.5\times 6.5=14.65\)
商の対数の公式より
\(\log_{10}E_{2}-\log_{10}E_{1}=\log_{10}\begin{aligned}E_{2}\\ \overline{E_{1}}\end{aligned}\)
従って
\(=\log_{10}\begin{aligned}E_{2}\\ \overline{E_{1}}\end{aligned}=1.65\)
\(\dfrac{E_{2}}{E_{1}}=10^{1.65}=44.7\)
・令和6年能登半島地震の地震エネルギーは
⇒令和5年能登半島 群発地震(2023年5月5日)の
⇒45倍

■震源断層面とマグニチュードの関係
◆令和6年能登半島地震(2024年1月1日)
・マグニチュード(Mj):7.6
・最大震度:7
・深さ:16km
・断層がずれた長さ:約150km(北東から南西に延びる)
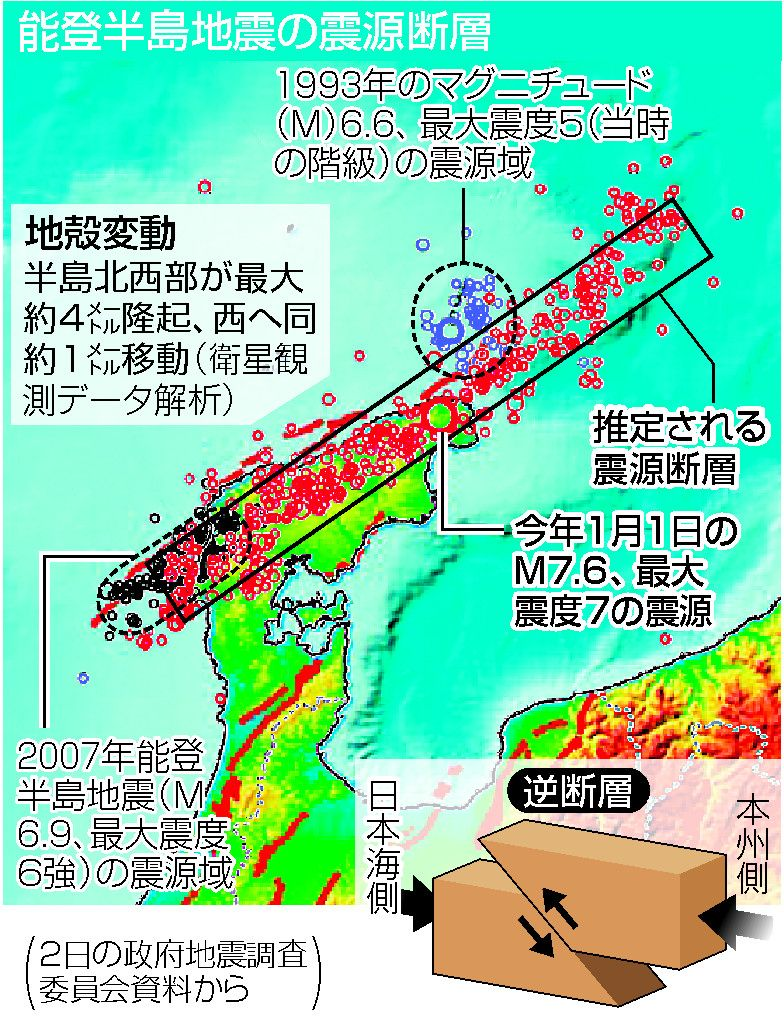
出典:JIJI.COM 2024.2.24
◆ローカルマグニチュード\(M_{L}\)と「マグニチュードの飽和」
・米国の地震学者チャールズ・F・リッターによぅて1935年に提案された。
\(M_{L}=\log _{10}A\)
と定義され、ここでAは地震計で観測される最大振幅を表す。
この値によって地震の大きさを客観的に規定できるようになった。
・マグニチュードの飽和
⇒ローカル・マグニチュードを使用して測定を行う場合
\(M_{L} >6\)
⇒の地震はすべてマグニチュード6の地震として誤認されてしまう。
⇒つまり、ローカル・マグニチュードによる計測では
⇒マグニチュードの値が頭打ちになってしまう。
⇒これを「マグニチュードの飽和」と呼ぶ。
◆ローカル・マグニチュード(地震波の最大振幅に依存)の限界点
・地震が比較的短時間で完結する場合は
⇒地震計で観測される地震波の振幅を用いるだけで
⇒ある程度の地震の規模を見積もることができる。
・数十~数百キロメートルに渡る断層のズレが発生する巨大地震の場合は
⇒地震計で観測される最大振幅だけでは地震の規模を測れない。
⇒東日本大震災の被災地では震度4~5を超える揺れが数分間もの間ずっと続いた地域もあった。
⇒最大振幅が観測されるのは一瞬である。

出典:NHK
・巨大地震の場合は
⇒エネルギーの放出が長時間続くために
⇒最大振幅を測るだけでは
⇒地震の規模を正しく計測できない。
◆モーメント・マグニチュード\(M_{W}\)
・1979年、マグニチュードの飽和を解決するための新しい指標\(M_{W}\)が提案
⇒地震計で記録された地震波の振幅ではなく
⇒地震モーメント(\(M_{0}\))に基づいて計算される。
⇒モーメント・マグニチュード\(M_{W}\)は、
⇒最も破壊的な地震(マグニチュード8以上)のマグニチュードを
⇒確実に測定できる尺度であり、今なお世界中で広く用いられている。
・地震モーメント(\(M_{0}\))
断層面の剛性率:\(\mu\left( Pa\right)\)
断層面積の合計:\(A\left( m^{2}\right)\)
断層全体の変位(すべり)量の平均:\(\overline{D}\left( m\right)\)
地震モーメント:\(M_{0}=\mu A\overline{D}\)
と表される。この値の単位はニュートンメートル(N・m)で
トルク(=力のモーメント)と同じ。
・モーメント・マグニチュード\(M_{W}\)は
\(M_{W}= \dfrac{2}{3}\log _{10}M_{0}-10.7\)
という式で定義される。
このようにして、地震波の最大振幅に依存しないマグニチュードが定義された。
これにより、マグニチュード9程度の巨大な地震であっても
正しく規模(エネルギー)を見積もることが可能となった。
以上の情報の出典:マグニチュードを理解しよう【地震の数理】2020年6月27日 投稿者:PENCIL
◆断層の大きさとマグニチュード
・マグニチュードは『断層の大きさ』に比例する
⇒マグニチュードが1増えれば、断層の長さや幅が約3.16倍になる(面積はほぼ10倍)。
⇒更に、断層がずれ動く長さも約3.16倍になるため
⇒地震により断層から放出されるエネルギーは『面積×ずれ動く長さ』でほぼ32倍(=3.16^3)
・震源断層面積比較
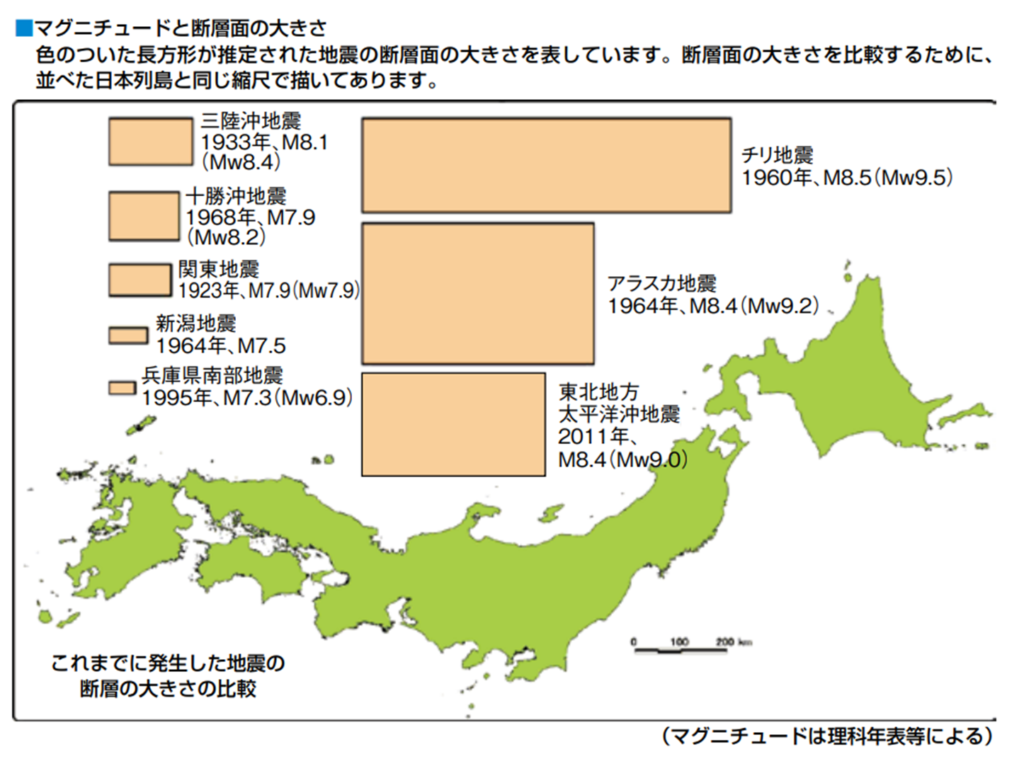
出典:https://www.jishin.go.jp/main/pamphlet/wakaru_shiryo2/wakaru_shiryo2_4.pdf 地震が分かる!解説編 第1部地震の仕組みと現象
※気象庁マグニチュード:Mj(M)、モーメントマグニチュード:Mw(世界標準指標)
・震源の深さと震源域(震源断層面)
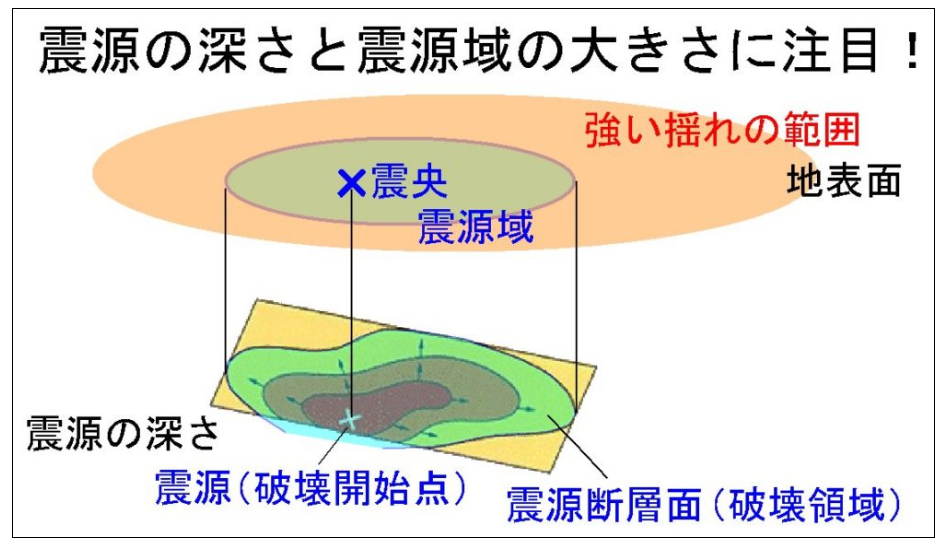
・震源断層面積(長さ×幅)とずれ量(すべり量)
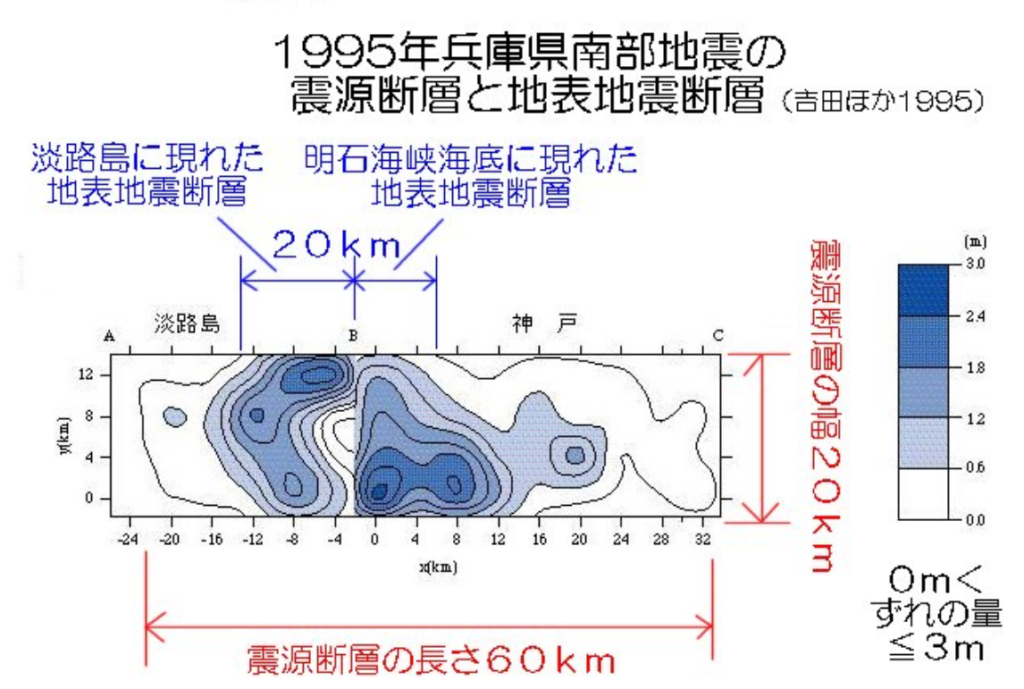
出典:https://mtl-muse.com/study/earthquake/sourcefault/ 大鹿村中央構造線博物館
・令和6年能登半島地震の震源断層モデル(暫定:2024年1月15日時点)よりモーメントマグニチュードMwの算出
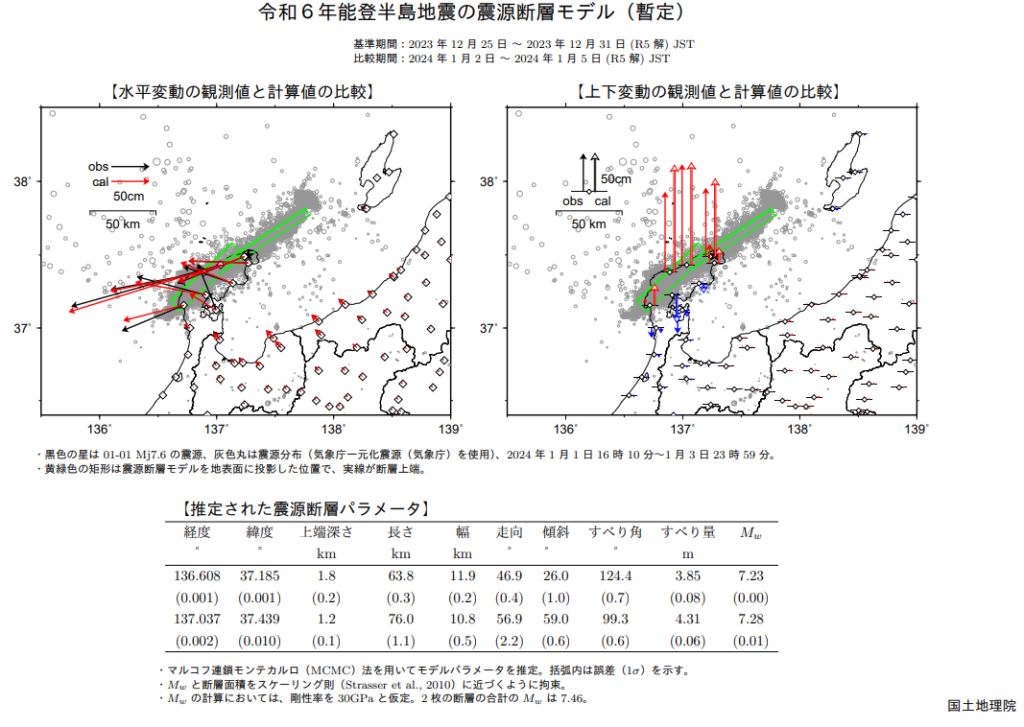
出典:https://www.gsi.go.jp/common/000254306.pdf 国土交通省 国土地理院 【参考】2024年1月15日時点の震源断層モデル
・上記【推定された震源断層パラメータ】を利用して『Mw』の再確認

計算サイト:https://keisan.casio.jp/exec/user/1528155818
■2020年頃から始まった能登半島群発地震を観測・マグニチュード7前半の予想も含めた専門家談
・珠洲市周辺で約7センチ隆起する地殻変動をGPS網を利用して特定していた
⇒地下にて火山活動をしている地域以外では異常な動きである
⇒何かが地盤を持ち上げている
⇒珠洲市周辺の地下にて流体(水の存在)が上昇して
⇒地殻隆起を起こしていると仮説を立てていた。
・水の存在を想定(電気を通しやすい領域)して
⇒能登半島の地下を観測し、水の存在が北側の領域に向かって続く観測データを確認した。
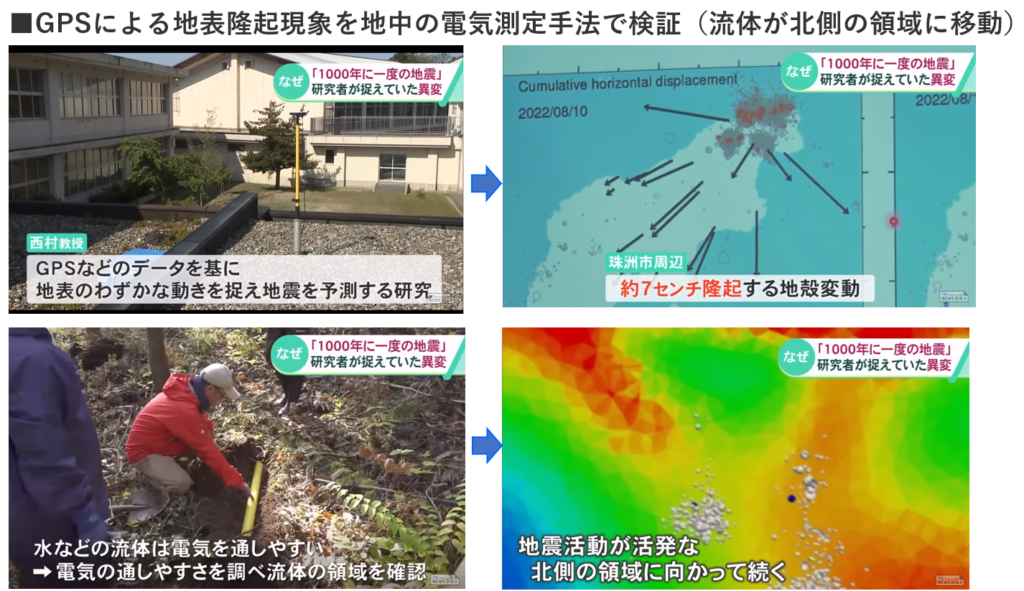
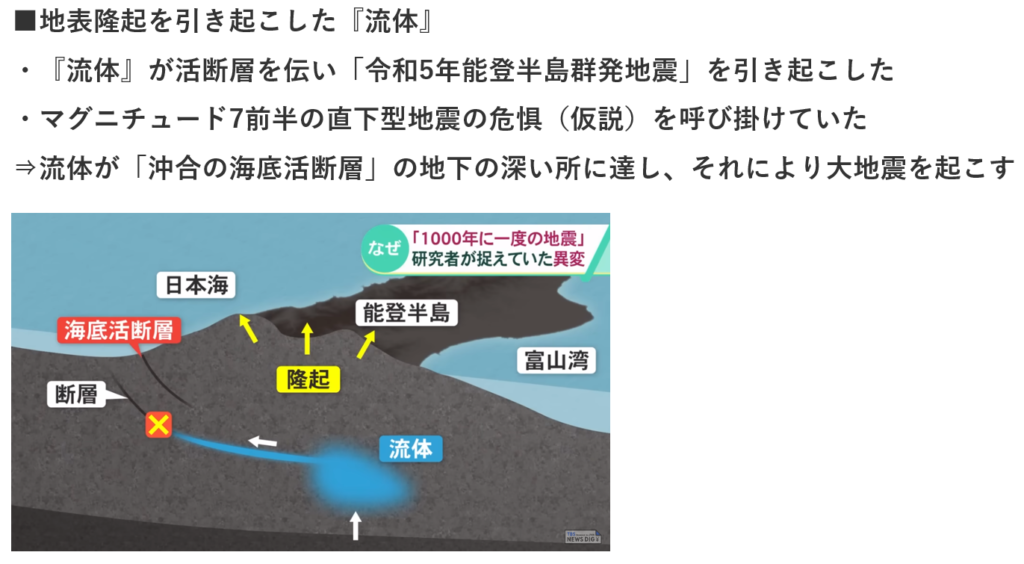
出典:“1000年に一度の地震” 専門家「ワーストシナリオの中でも予想上回る」 能登半島地震の発生メカニズムを解説|TBS NEWS DIG
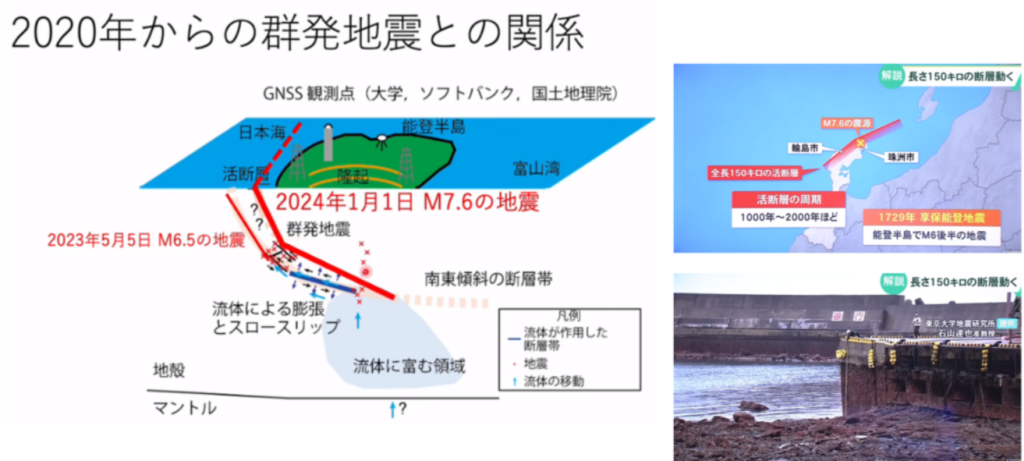
出典:左図)https://www.youtube.com/watch?v=Dx1xf-22ODM 右図)「ワーストシナリオの中でも予想上回る」
◆地震研究の専門家の情報発信を真摯に聴く
・発生時期は特定されなくとも
⇒発生メカニズム(仮説)の説明内容は信頼性が高いことを上記YouTubeでも確認。
⇒想定外を想定出来る環境は有る。
尚、産業技術総合研究所 活断層・火山研究部門 寒川 旭 名誉リサーチャーの一連の動画において、 将来能登半島で大きな地震が起きることを述べていた。
出典:出典:https://kansai.main.jp/swfu/d/jishin20230606.pdf (寒川 旭 氏のPDF資料より)
出典:https://www.npo-lso.or.jp/earthquake/index.html
<参考情報:岩手・宮城内陸直下型地震:2008年>
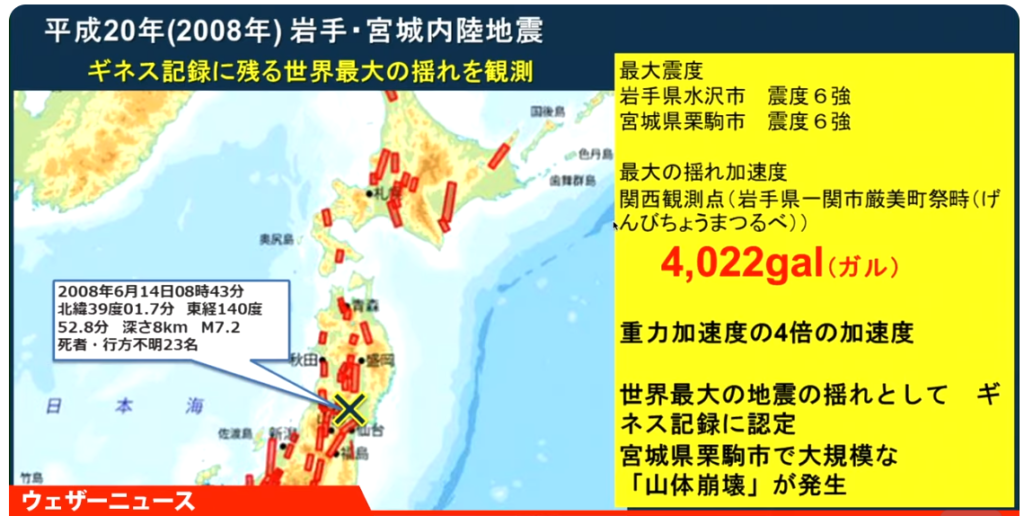
・岩手県沿岸北部でM6.1 震度5弱 2024年4月2日(火)
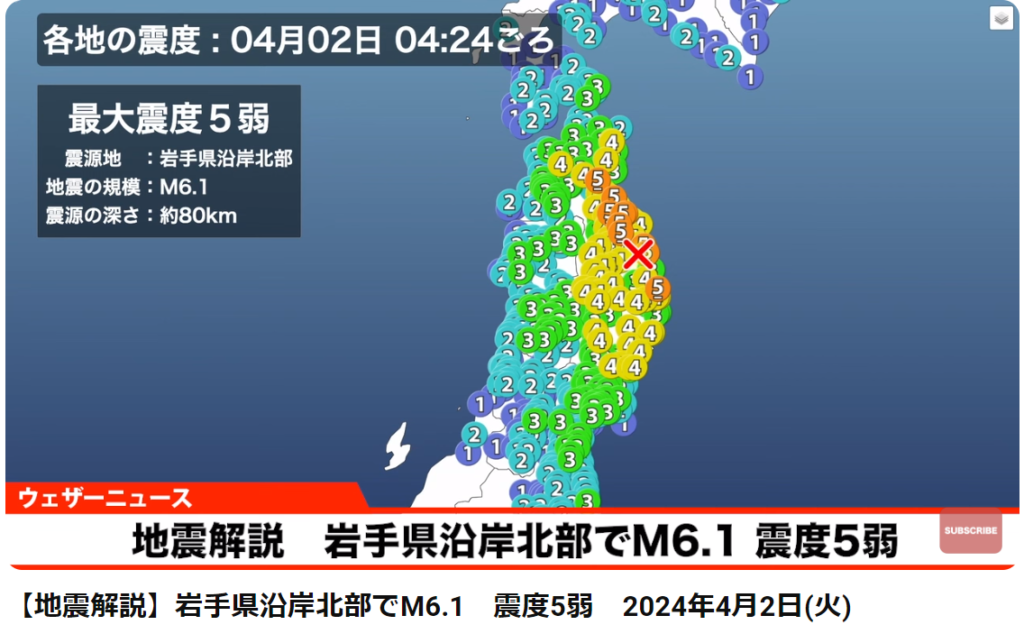
出典:ウェザーニュース
出典:https://www.duma.co.jp/blank-4
・マグニチュード5(E₁)と6(E₂)を比べる
\(\log_{10}E_{2}=4.8+1.5\times 6=13.8\)
\(\log_{10}E_{1}=4.8+1.5\times 5=12.3\)
商の対数の公式より
\(\log_{10}E_{2}-\log_{10}E_{1}=\log_{10}\begin{aligned}E_{2}\\ \overline{E_{1}}\end{aligned}\)
従って
\(=\log_{10}\begin{aligned}E_{2}\\ \overline{E_{1}}\end{aligned}=1.5\)
\(\dfrac{E_{2}}{E_{1}}=10^{1.5}=31.62\)
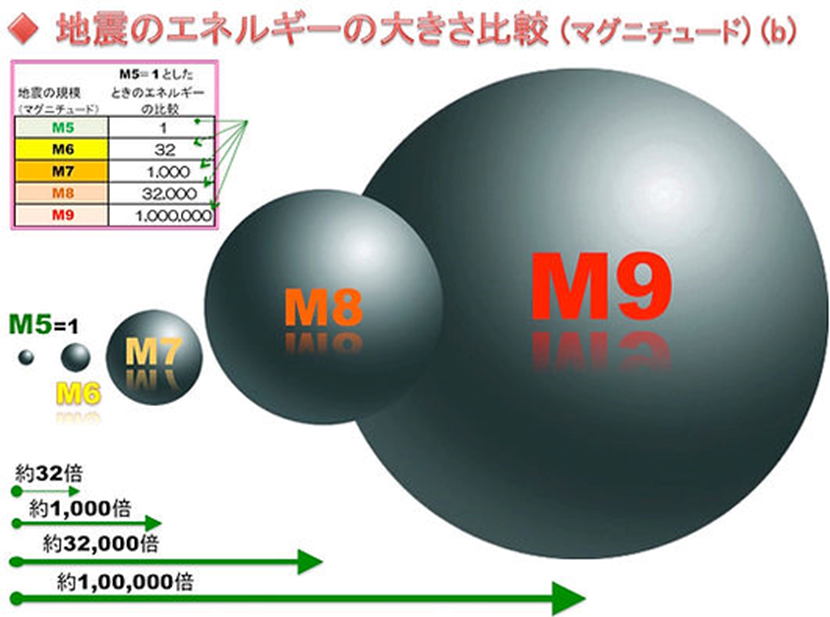
・マグニチュード(M)が1つ増えると、地震のエネルギー(E)は約32倍のエネルギーになる
\(32^{2}=1024\)、\(32^{3}=32768\)、\(32^{4}=1048576\)
出典:https://www.eri.u-tokyo.ac.jp/YOTIKYO/OpenReport/H30/H30SeikaGaiyo.pdf 「災害の軽減に貢献するための地震火山観測研究計画」平成30年度年次報告 科学技術・学術審議会測地学分科会 地震火山部会
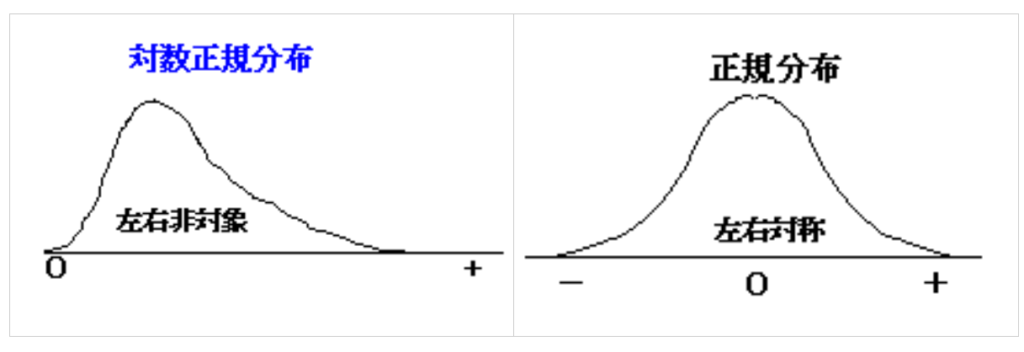
■ベキ分布と正規分布の特徴
◆正規分布
⇒人間の伸長、テストの成績等
⇒平均、分散が存在する
◆ベキ分布
・規模(サイズ)と個数(発生頻度)の分布
・分布が左右対称になる正規分布とは対照的に
⇒中央値・最頻値が分布の左端に位置する。
⇒平均や分散という概念が事実上意味をなさないという点で、正規分布とは異質なる。
・どの尺度で拡大・縮小しても
⇒常に同じような分布になるという「スケールの不変性」がある。
・統計的な意味
⇒平均や分散が存在しない確率分布である。
⇒そのような確率分布では中心極限定理は成立せず、標本数を幾ら大きくしても標本平均は正規分布に従わない。
⇒検定では棄却域に入る部分は「滅多に起きない」ものとして棄却されるが、大地震のように滅多に起きない棄却域部分こそ重要な場合がある。
⇒正規分布や中心極限定理だけを念頭に置いて考えるとは問題がある。
■フラクタル(スケールを持たない系)
・ベノワ・B・マンデルブロ博士が作り出した言葉
⇒特徴的な長さを持たない図形や構造はフラクタルと総称されている。
⇒コッホ曲線や海岸線、血管の複雑に枝分かれした構造にも特徴的な長さがない。
⇒特徴的な長さには滑らかな面(微分が出来る)がある(例:直方体、球、円筒、曲面等)。
⇒フラクタル=特徴的長さがない=滑らさが無い=微分が出来ない形(形状)を取り扱う。
・パレートの法則(\(P\left( x\right) =cx^{-a}\))
以下の内容は下記URLより転記
http://kj01.kgu.mydns.jp/fujimoto/inen/kaisetu_pareto.html
⇒\(x\)は所得金額、\(c\)は定数、\(P\left( x\right)\)は所得金額\(x\)の番付け(上位から数えた累積人数)
⇒\(y=P\left( x\right)\)を書き直して
⇒\(y=cx^{-a}\)
⇒両辺で対数を取る
⇒\(\log _{10}y=\log _{10}\left( cx^{-a}\right)\)
⇒\(\log _{10}y=\log _{10}c+\log _{10}x^{-a}\)
⇒\(\log _{10}y=log _{10}c-a\log _{10}x\)
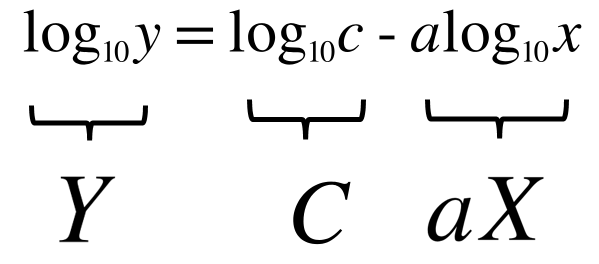
と置くと
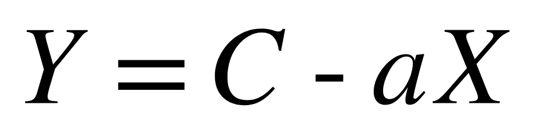
となり、\(x\)軸、\(y\)軸共に対数の場合に一次式(線形)になる。
⇒対数軸を使うと、パレートの法則は傾き\(-a\)の直線として表現できる。
・スケールを持たない系(\(P\left( x\right) =cx^{-a}\))
⇒ \(x\) → \(10x\) としてみる
⇒ \(cx^{-a}\) → \(c(10x)^{-a}\)
⇒ \(c(10x)^{-a}\) = \(c\left( 10\right) ^{-a}x^{-a}\) = \(c^{`}x^{-a}\)
⇒(ここで、\(c(10x)^{-a}\)を改めて\(c^{`}\)と書き直した)
⇒これにより、\(x\)のスケールを(10倍に)変えた場合も
⇒パレートとの法則を意味する数式は形を変えないことがわかる。
⇒すなわち、この数式で表される系には
⇒スケールが存在しない。
⇒スケール変換をしても
⇒形を変えない分布はこの関数形しか存在しなことも証明できる。
◆フラクタルとは?
・自己相似になっている系をフラクタルと呼ぶ。
⇒複雑に見える図形の小さな部分を拡大すると
⇒全体(より大きな部分)と同じような形になっている(拡大しても同じ形が繰り返し現れてくる形)。
⇒この複雑さを評価する指標として『フラクタル次元(=複雑性の度合い)』が考えられた。

・同じパターンが繰り返される系とは
⇒あるパターンを見てもその大きさ(スケール)が分からないことを意味する。
⇒つまり、大きなスケールでも小さなスケールでも同じように見える。
■地震予知の否定も導くベキ分布の「スケール不変性(フラクタル性)」
・ベキ分布の法則は岩を砕いたときの破片の大きさの分布にも見られる
⇒割れた岩はいくつかの大きな破片と無数の小さな破片に分解される。
⇒その無数の小さな破片を拡大すると、やはり数個の大きな破片と無数の小さな破片に分けられる。
⇒両者の違いは拡大縮小の違いであり
⇒両者を分け隔てる物理的メカニズムは存在しない。
⇒大きな地震と小さな地震との間に特徴的な違いはなく、大地震の兆候といった特別な要因も存在しない。
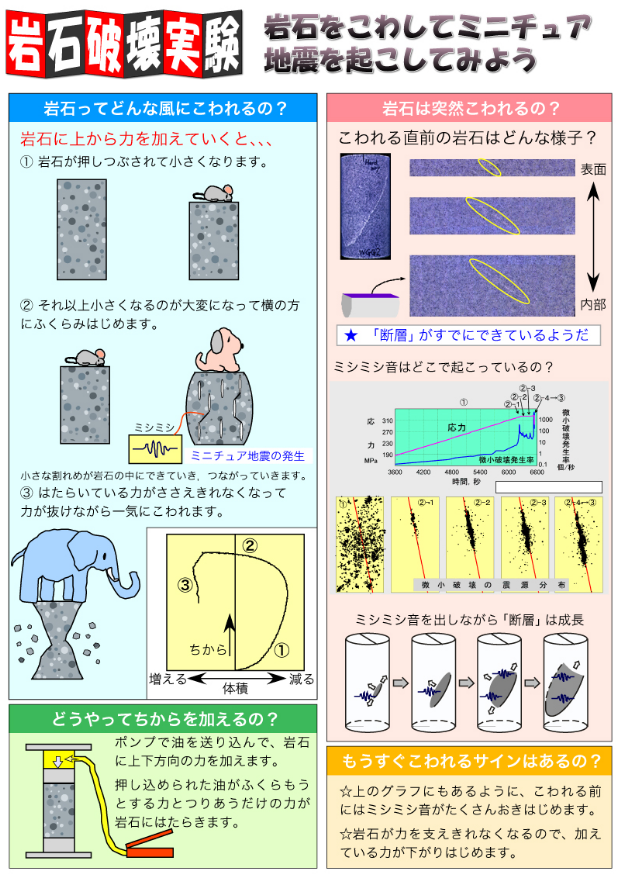
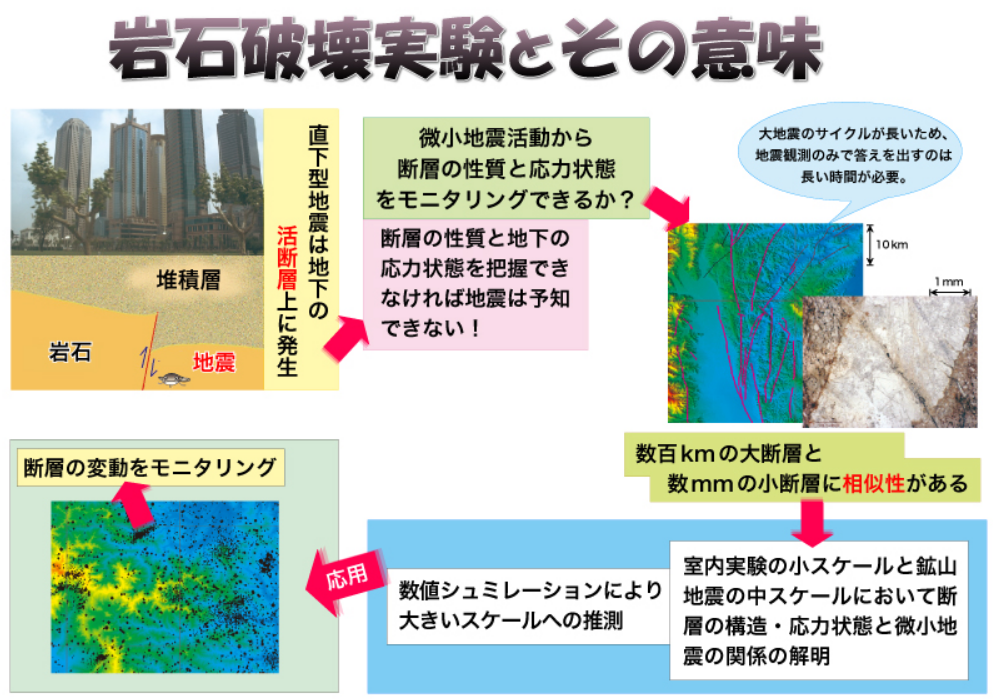
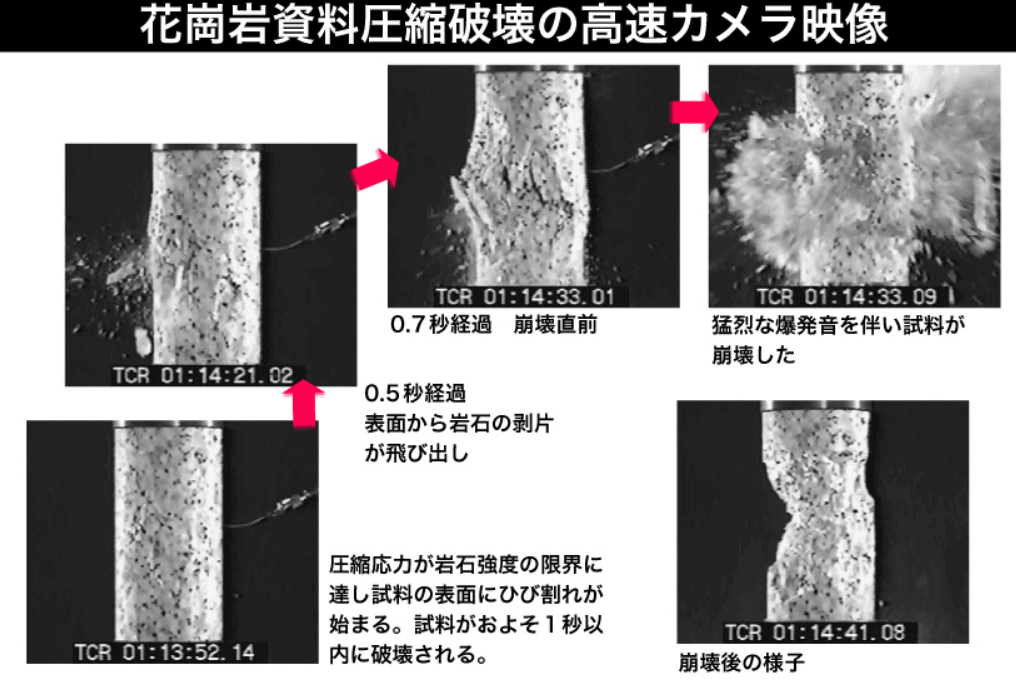
出典:https://www.gsj.jp/researches/openfile/openfile2008/b015.html 産総研 地質調査総合センターB015 岩石破壊実験
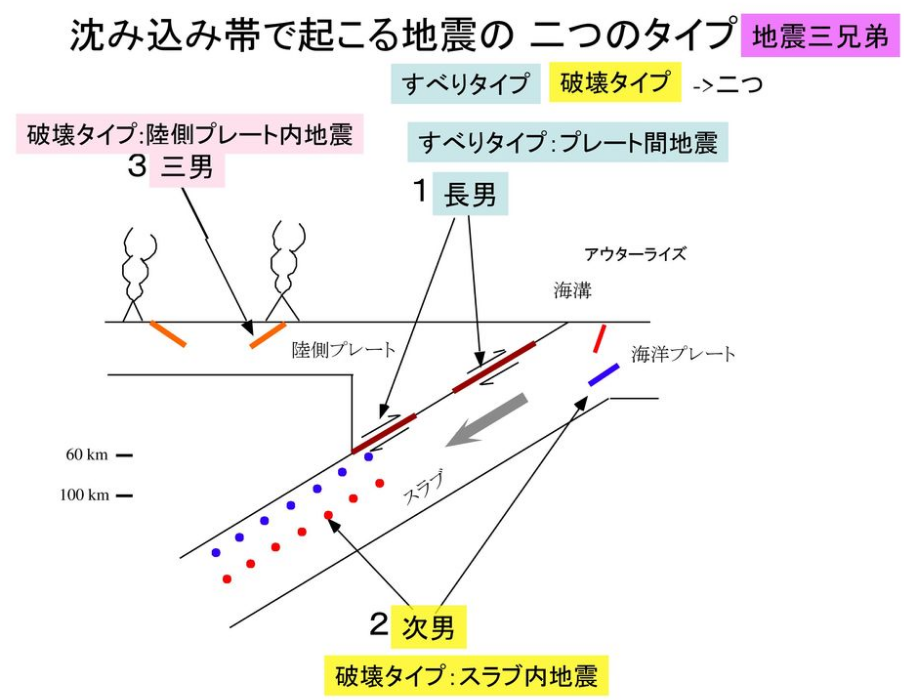
出典:https://slidesplayer.net/slide/11572045/ 首都圏および東葛地域の地震について 瀬野徹三(東京大学地震研究所) 2012.09.29布施新町二自協ふれあいセミナー
■統計的仮説検定とは
・母集団の分布の母数(θ)に関する仮説の妥当性を
⇒標本から検証する方法
◆仮説検定の論理(帰無仮説 対 対立仮説)
・帰無仮説:『仮説は正しくない』を表現する仮説
⇒否定される事を前提に立てられている
・対立:『仮説は正しい』を表現する仮説
⇒帰無仮説に対して排反的な仮説
⇒1つの帰無仮説に対して、対立仮設は複数考えられる事に注意
例:
・仮説検定の論理
◆検定統計量
・仮説検定で使用する統計量
⇒帰無仮説を表現する検定統計量の分布と実際の観測地とのズレの大きさを図る為に使用
例:
・検定統計量に
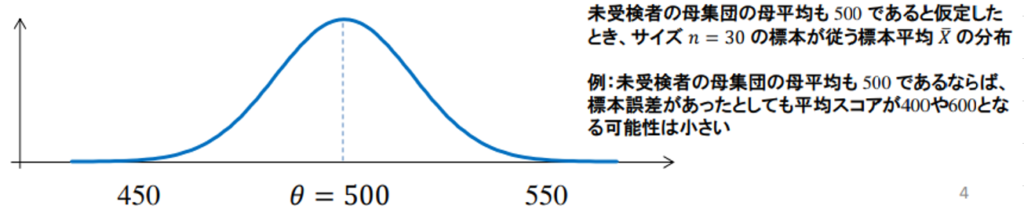
⇒標本平均\(\overline{x}\)を用いる
・帰無仮説:・・・差はない
・対立仮説:・・・差はある
帰無仮説が成立すると仮定した時の検定統計量\(\overline{x}\)の分布の例(正規分布)
◆棄却域と有意水準
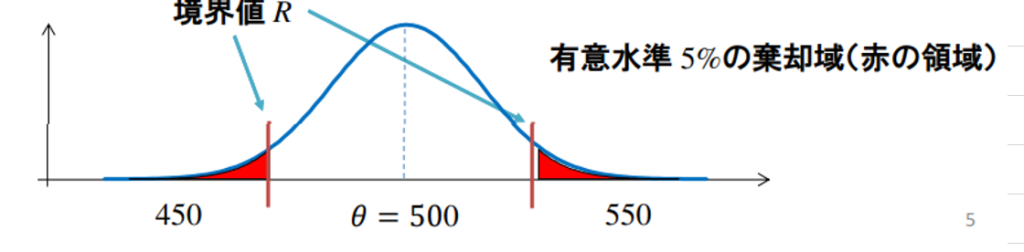
・棄却域:帰無仮説から離れたある領域
・有意水準:ある事象が起こる確率が偶然とは考えにくいと判断する基準となる確率
⇒検定統計量の分布(確率密度関数)の棄却域での面積
⇒5%や1%を設定
⇒境界値:棄却域と境界線の値
帰無仮説が成立すると仮定した時の検定統計量\(\overline{x}\)の分布の例(正規分布)
◆帰無仮説の棄却と解釈
・帰無仮説の『棄却』
⇒帰無仮説は統計的に認められないという結果(例:5%有意水準で棄却)
⇒対立仮説が採択される
・帰無仮説が棄却された場合
⇒対立仮説が統計的に認められる
・帰無仮説が棄却できない場合
⇒対立仮説に関して何も分からない
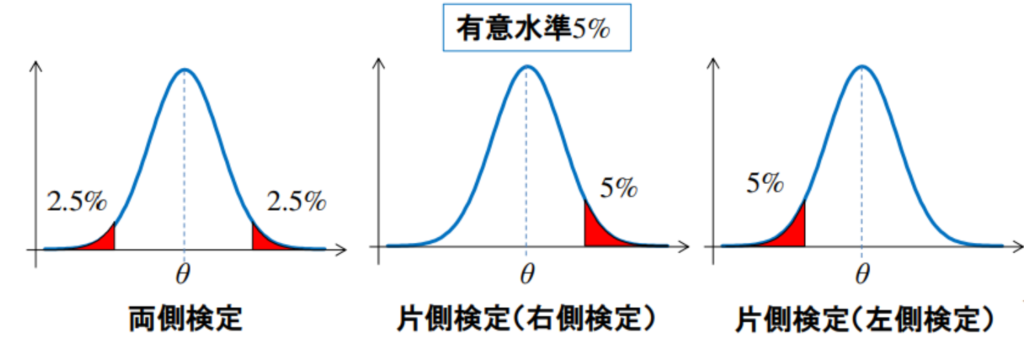
◆両側検定と片側検定(1)
・両側検定:棄却域を分布の両端に定める
例
・片側検定:棄却域を分布の片側に定める
例:・・・・・平均的に高いか(右側検定)
例:・・・・・平均的に低いか(左側検定)
◆両側検定と片側検定(2)
・帰無仮説H₀と対立仮説H₁の立て方
・θは母集団の母数の値(例: )
・θ₀は帰無仮説での母数の値(例: )
⇒両側検定 H₀:θ=θ₀、H₁:θ≠θ₀
⇒右側検定 H₀:θ=θ₀ or θ≤θ₀、H₁:θ>θ₀
⇒左側検定 H₀:θ=θ₀ or θ≥θ₀、H₁:θ<θ₀
◆検定の手順
1.仮説を立てる
2.検定統計量を定める
3.有意水準α(5%や1%)を定める
4.標本から検定統計量を計算
5.検定統計量の分布(例:正規分布のような近似検定用分布)から棄却域を定める
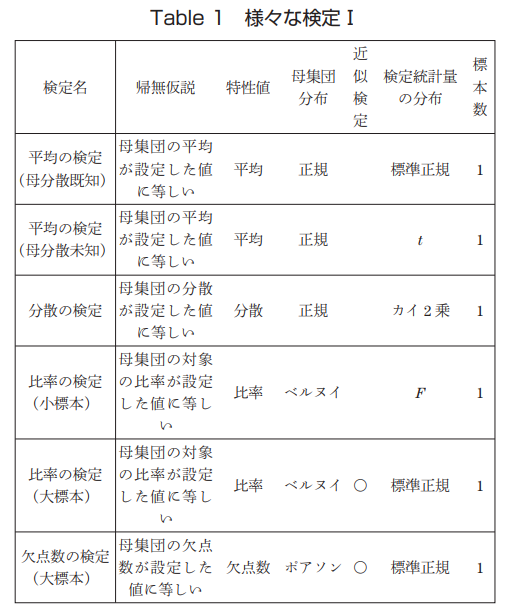
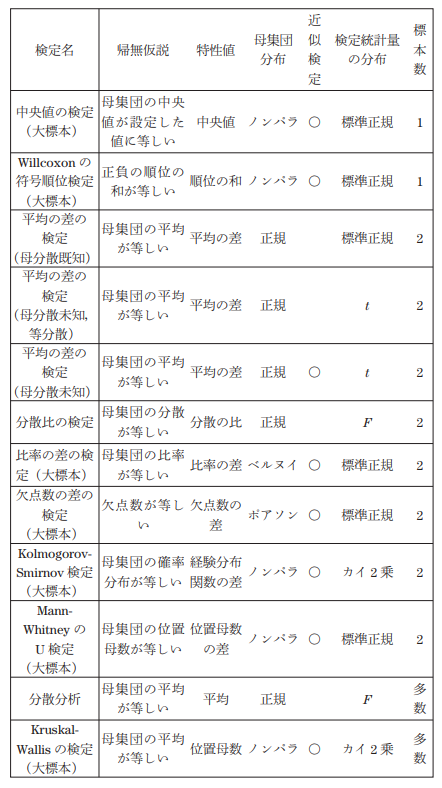
出典:https://www.jstage.jst.go.jp/article/konpyutariyoukyouiku/34/0/34_24/_pdf/-char/ja
6.帰無仮説を棄却できるかを検定
◆検定の例(1)
1.仮説を立てる
⇒帰無仮説:「・・・ではない」H₀:θ=θ₀
⇒対立仮説:「・・・である」H₁:θ>θ₀
・・・・・・・・・検定
・θ₀:・・・・・・・・・・・・・・理論値
・θ:・・・・・・・・・・真の母数から計算される・・
2.検定統計量をXを定める
・・・確率変数

・nが大きいので中心極限定理より正規分布で近似
3.有意水準を決める
・5%有意水準(α=0.05)の片側検定(右側検定)
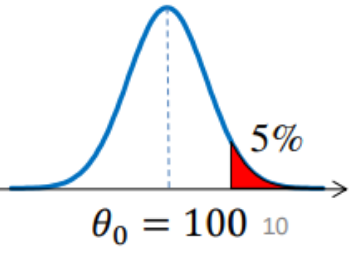
4.標本から検定統計量を計算

5.検定統計量の分布(標準正規分布)から棄却域を求める

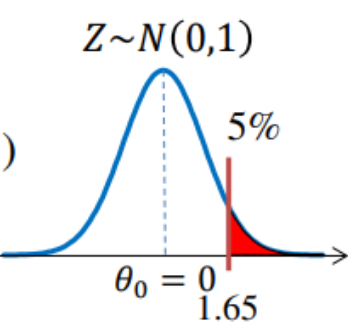
6.帰無仮説を棄却出来るかの検定

◆検定の誤り
・第1種の過誤
⇒本当は帰無仮説を棄却できないのに、検定では棄却していまう間違え
⇒P(帰無仮説を棄却する|帰無仮説が正しい)=α(αは有意水準)
・第2種の過誤
⇒本当は帰無仮説を棄却できるのに、検定では棄却できない間違い
⇒P(帰無仮説を棄却できない|対立仮説が正しい)=β
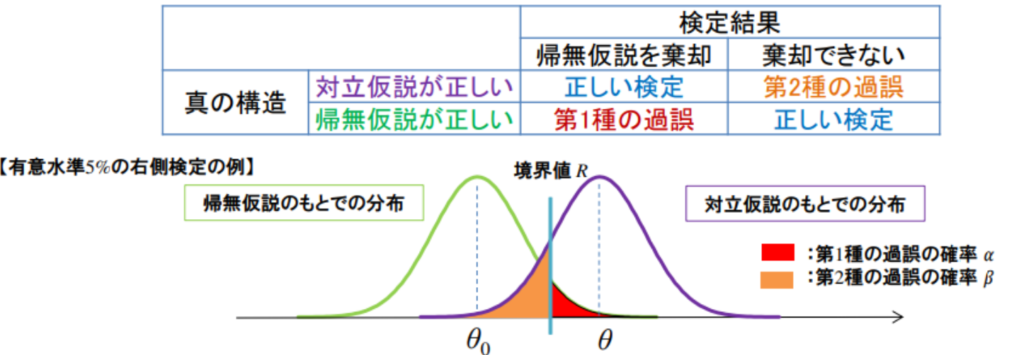
注:第Ⅰ種過誤と第2種過誤を同時に小さくする事は出来ない。
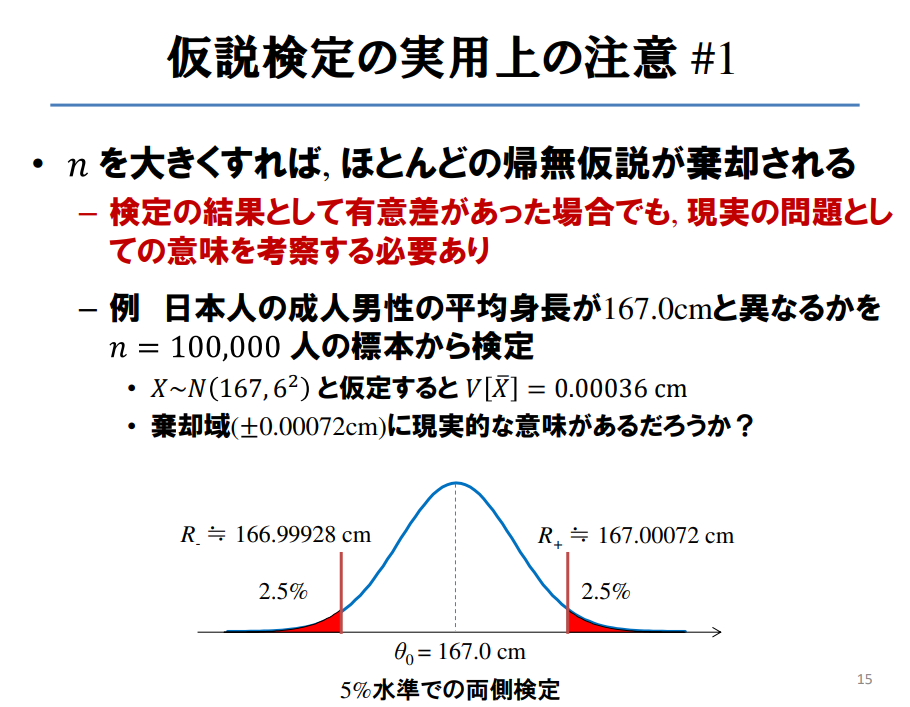
◆P値
・観測された有意水準
⇒P値が事前に設定された有意水準αよりも小さければ
⇒帰無仮説は棄却できる
・検定の結果
⇒あらかじめ与えられた有意水準αで棄却できるか否かであり
⇒P値が小さい方が
⇒より強く棄却されるわけではない事に注意


■部分的知識下における火山噴火時の避難指示意思決定論に関する研究~平成25年2月21日 京都大学工学部地球工学科土木コース 西本 恒 氏の論文を転記~
■避難指示意思決定時の仮設検証
・噴火の被害を受ける可能性がある地域住民に対して
⇒避難指示を出すか出さないを判断する際、
⇒噴火の被害が及ぶという仮説を受け入れるか、棄却するか
・仮説検定時における2種類の誤り
①仮説が真である時に
⇒それを棄却してしまう誤り。第1種の誤り。
②仮説が偽りである時に
⇒それを受け入れてしまう誤り。第2種の誤り。
■噴火の場面で、仮に仮説を『地点Aに災害が及ぶ』というもにすると
・第1種の誤りとは
⇒地点A噴火の被害が及ぶにも関わらず
⇒地点Aの住民や滞在者に対して避難指示を出していなかったために(棄却)
⇒生命や身体に致命的な被害を受けることを意味する。
・第2種の誤りは
⇒地点Aには噴火の被害が及ばないにも関わらず
⇒地点Aの住民や滞在者に対して
⇒避難指示を出しており、
⇒その避難指示が結果的に空振りに終わるという誤りを意味する。

・この火山噴火時の仮説検定は表ー2.1のように表される
⇒避難指示意思決定を行う場合には
⇒これら二種類の誤りが起こりうることを考慮しておく必要がある。
・災害発生初期から火山の噴火活動が収まるまでの期間(例:1707年宝永噴火では12月16日~12月31日)において
⇒避難指示に関する意思決定を行う際、
⇒第1種の誤りと第2種の誤りとでは
⇒その誤りの重みには大きな差があると考えられる。
■避難指示の意思決定
・第一の目的は
⇒住民や滞在者の生命や身体に致命的な被害を及ばないようにすること。
・非難指示の空振りに終わる損失を減少することは
⇒副次的な目標である。