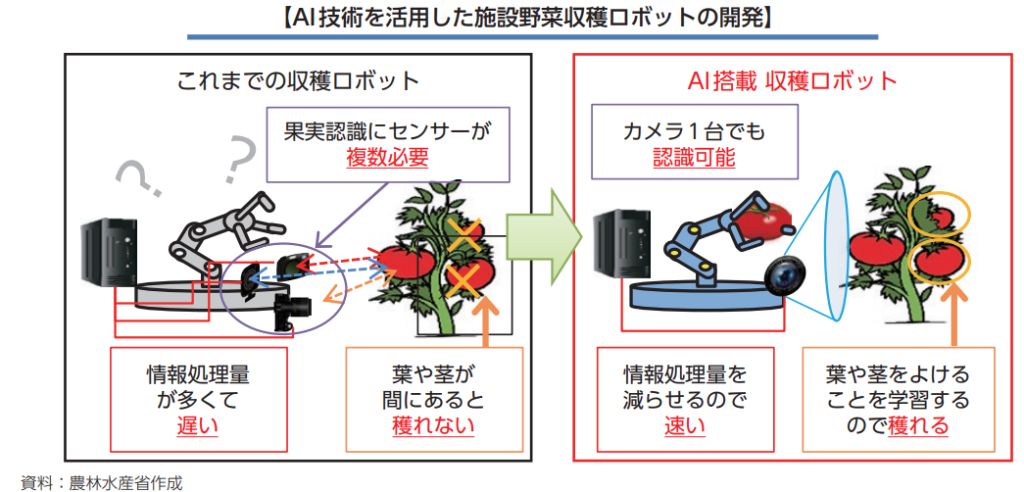
作物が健全に生育するための要素は非常に複雑であるが、どのような生育予測モデルが可能かを検討する。予測モデルが実用的であれば、次の行動が具体化できる事はメニュー『施設園芸のPDCA~植物工場』で記載した(有)育葉産業様の事例で容易に推測できる。
複雑さの一例として『土づくり(土壌管理)』と『気候環境(例:平均気温の上昇がもたらす収量の影響)』を取り上げる。
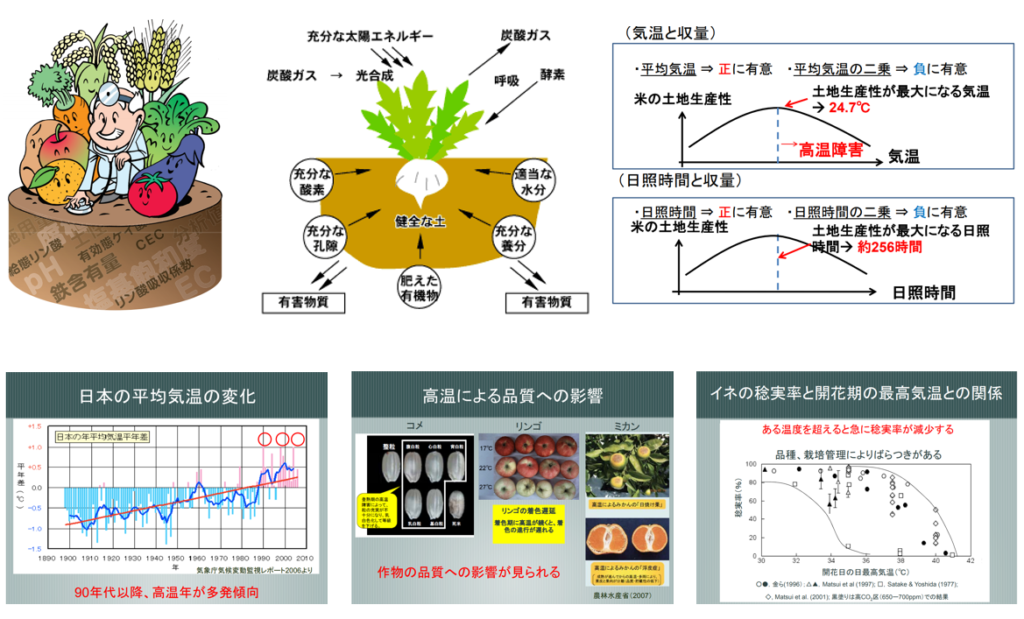
単独の指標(平均気温の上昇)から結論として『高温による品質の影響』を導くのは説明しやすい。
非常に多様な要因が複雑に絡み合う農作物の生育過程をどのような視点で予測モデル表現ができるかが今回のテーマである。
アップルのCDO(最高デザイン責任者) ジョナサン・アイブ氏のデザイン哲学を手掛かりにする。iOS7発表の際、アイブ氏のビディオメッセージで以下の発言が当時、大きく話題になった。
シンプルであること、明快であること、効率的であることには、それぞれ奥深く、不朽の美しさがある。 「真のシンプルさは混乱や虚飾を廃することからは生まれません。 それは複雑性のなかに秩序をもたらすことなのです」。
氏のメッセージに刺激を受け、『秩序の導入』として生育予測モデルをロジスティックス方程式(微分方程式)で表現してみよう。
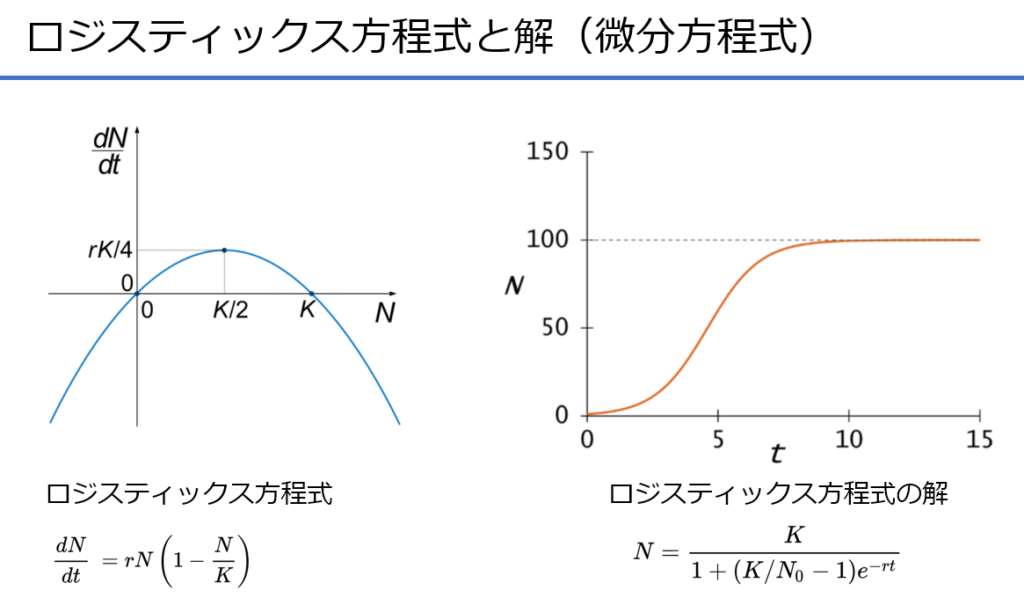
ロジスティック方程式 は上記の微分方程式で表される。
N は個体数、t は時間、dN/dt が個体数の増加率を意味する。r は内的自然増加率、K は環境収容力と呼ばれる定数である。
個体数(N)が増えて環境収容力(K)に近づくほど、個体数増加率(dN/dt)が減っていくというモデルになっている。 ( Wikipediaより)
農産物の生育予測モデルとしてロジスティック方程式を利用した事例を以下に紹介する。
下記事例は、 IoT を利用して,ベビー リーフにおいて製品含有率の高い周年多回転栽培作物のピノグリーンを生産している圃場からデータを収集し, 得られたデータから,播種後の経過時間と単収値,および,生育値の関係を明らかにしたと記載されている。
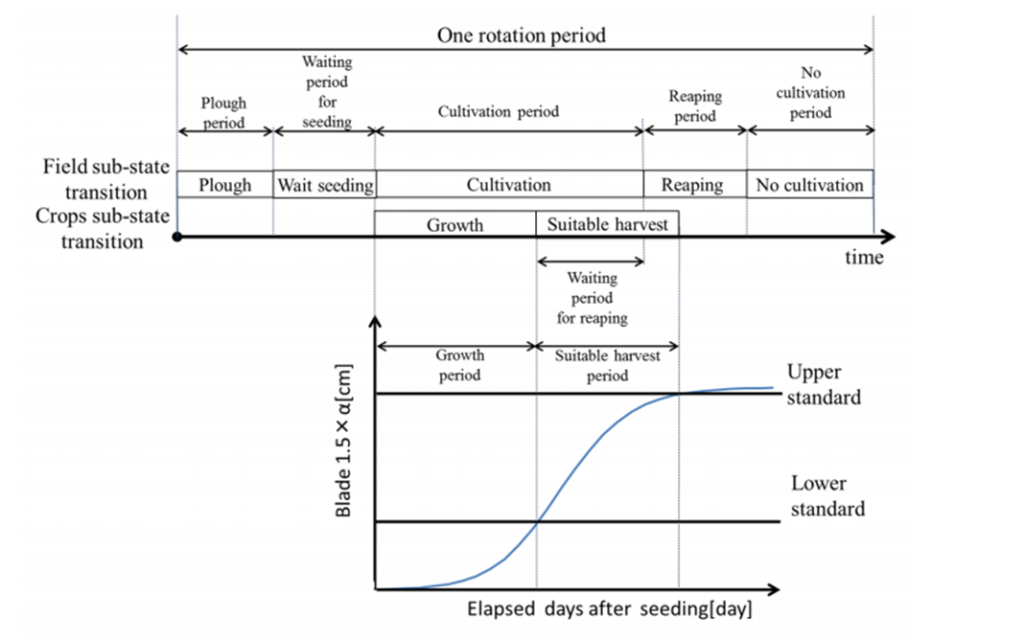
(日本機械学会論文集 Vol.85, No.872, 2019 )
【圃場サブ状態】 養生状態 Plough :圃場環境を整え,作物生育のための準備をする状態 播種待機状態 Waite seeding :養生を終え,播種が行われるまでの待機状態 栽培状態 Cultivation :播種から刈取までを表す,圃場に作物が存在する状態 刈取状態 Reaping :圃場で生育した作物に対して刈取を行っている状態 休耕状態 No cultivation :刈取が終了してから次回の養生が行われるまでの待機状態 【作物サブ状態】 生育状態 Growth :播種後,作物の生育値が出荷基準を満たすまでの状態 刈取適期状態 Suitable harvest:作物の生育値が出荷基準を満たしている状態 生育超過状態 Unsuitable harvest:作物が出荷基準を超えて生育した状態
■IoT に基づく作物の生長プロセスの分析■
圃場での IoT の利用、センサーで取得する情報は,湿度,気温,地温,散水量, 日照量である.各センサーでは,30 日間,30 分毎に計測を行った.センサーでの取得が難しい生育値,単収値の 情報は人手で 30 日間,50 サンプル計測した.生育値 h cm は,葉長α(図 3 参照)を利用して式(1)で表す.得られた実測生育値を用いた実測生長曲線の近似曲線の推移を図 3 に示す.図 3 より,刈取予定日における実際の生長値(生育値)が明らかになった.
h = 1.5×α (1)
近似曲線と実測生長曲線の寄与率は 0.99 であり,実測生長曲線は,ロジスティック関数に近似できることが分 かった.作物の生長曲線は一般的にロジスティック関数に近似される(松田他,2011,佐藤,高橋,2002,土崎, 2011)ロジスティック関数の一般式を式(2)に示す.実際の圃場から得られた近似生長曲線式を,式(3)に示す.

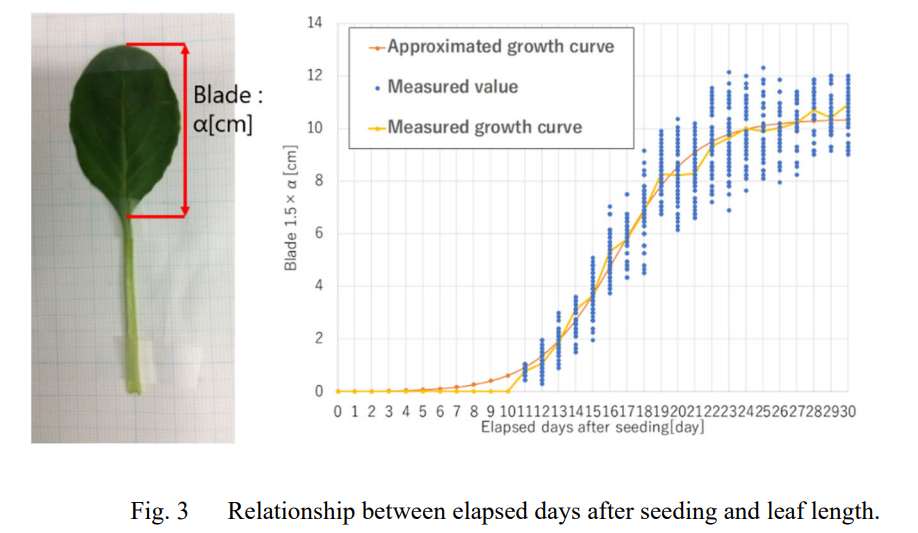
(日本機械学会論文集 Vol.85, No.872, 2019 )
その他、 『生育値と単収値の関係 』、 『欠品,および,優良ロスの事前評価シミュレーション手法 』等が記載されている。詳細内容はメニュー『Link』 ■栽培予想モデル~ロジスティックス方程式等 関係■上記出典を確認して下さい。
生育予測モデルとして『ロジスティックス曲線』で予測する手法も検討に値すると考える。単純化された前提条件でも複雑な要素(要因)が絡み合う現実を簡単な図式で表現でき、将来の『生育予測』も概ね分かる点に価値がある。
■ロジスティックス方程式の意味
\begin{aligned}\dfrac {dN}{dt}=rN\left( 1-\dfrac {N}{K}\right) \\ \end{aligned}
という微分方程式で表される。
- Nは個体数、
- tは時間、
- dN/dtが個体数の増加率を意味する。
- rは内的自然増加率
- Kは環境収容力と呼ばれる定数である。
個体数が増えて環境収容力に近づくほど、個体数増加率(dN/dt)が減っていくモデルになっている。
◆個体数(N)と増加率(dN/dt)との関係(=二次関数(幾何学的に解釈する)

\begin{aligned}\dfrac {dN}{dt}=rN\left( 1-\dfrac {N}{K}\right) \\ =rN-\dfrac {r}{K}N^{2}\end{aligned}
上に凸のグラフになる、
$$二次関数 \begin{aligned}y=ax^{2}+bx+c\\ \end{aligned} のグラフの頂点の座標を以下の公式を使い求める$$
$$\left( -\dfrac {b}{2a.}-\dfrac {b^{2}-4ac}{4a}\right) より$$
$$-\dfrac {r}{-2\dfrac {r}{K}}=-\dfrac {Kr}{-2r}=\dfrac {K}{2}$$
$$-\dfrac {r^{2}-4\dfrac {r}{K}\cdot 0}{-4\dfrac {r}{K}}=-\dfrac {Kr^{2}}{-4r}=\dfrac {Kr}{4}$$
N(個体数)=0とN=K( 環境収容力 )の時、dN/dt( 個体数の増加率 )=0になる。
個体数増加率 dN/dt の変化を見てみる。N が 0 から K/2 まで増えると、その間 dN/dt の値も増加し続ける。N = K/2 は放物線の頂点であり、ここで dN/dt は極大値を迎える。
N = K/2 を超えると dN/dt は減少し始め、N = K で 0 となる。
◆微分方程式の解
詳細な計算手順はメニュー『Link』の ■栽培予想モデル~ロジスティックス方程式等 関係■ ロジスティック曲線についての数学的補足 を参照願います。 http://rpe.y-imai.com/handouts/appendix_logistic-curve.pdf
\begin{aligned}\dfrac {dN}{dt}=rN\left( 1-\dfrac {N}{K}\right) \ \end{aligned}
を変数分離法にて解く
\begin{aligned}\dfrac {dN}{N\left( 1-\dfrac {N}{K}\right) }=rdt.\\ \dfrac {KdN}{N\left( K-N\right) }=rdt\end{aligned}
と変形し、左辺はN、右辺はtの関数に分離する。
左辺の分母が積になっているので部分分数分解して積分しやすくする。
$$\dfrac {KdN}{N\left( K-N\right) }=\left( \dfrac {1}{N}+\dfrac {1}{K-N}\right) dN$$
両辺を積分すると
$$ \int \dfrac {1}{N}dN+\int \dfrac {1}{K-N}dN=\int rdt $$
$$\log N-\log K-N=rt+c $$
$$ \log \dfrac {N}{K-N}=rt+c $$
両辺の指数をとる
$$ \dfrac {N}{K-N}=e^{rt+c} $$
Nについて解く。K-Nを両辺に掛ける
$$ N=e^{rt+c}\left( K-N\right) =Ke^{rt+c}-Ne^{rt+c} $$
$$ -Ke^{rt+c} を左辺に移項$$
$$ N\left( 1+e^{rt+c}\right) =Ke^{rt+c} $$
$$ 1+e^{rt}+c を両辺で割る$$
$$ N=\dfrac {Ke^{rt+c}}{1+e^{rt+c}} $$
となる。
$$右辺の分母、分子を e^{rt+c} で割ると$$
$$ N=\dfrac {K}{\dfrac {1}{e^{rt+c}}+1}=\dfrac {K}{e^{-rt-c}+1}=\dfrac {K}{1+e^{-c}\cdot e^{-rt}} $$
となる。
$$ e^{-c}=A と置くと$$
$$ N=\dfrac {K}{1+Ae^{-rt}} $$
これで解が求まった。
$$t=0の時の個体数を N_{0} とすると$$
$$ N\left( 0\right) =N_{0}=\dfrac {K}{1+A\cdot 1}=\dfrac {K}{1+A} $$
これをAについて解くと
\begin{aligned}1+A=\dfrac {K}{N_{0}}\\ A=\dfrac {K}{N_{0}}-1\\ =\dfrac {K-N_{0}}{N_{0}}\end{aligned}
となる。
よってロジスティックス方程式の解は
\begin{aligned}N=\dfrac {K}{1+Ae^{-rt}}=\dfrac {K}{1+\dfrac { K -N_{0}}{N_{0}}e^{-rt}}\\ =\dfrac {\ K }{1+\left( \dfrac {K} {N_{0}}-1\right) e^{-rt}}\end{aligned}
■ ■ロジスティックス方程式 の応用例:普及曲線■■
生産性の向上は一般にプロセスイノベーションでもたらされる。
1990年代のバブル崩壊下で元日産のゴーン社長に代表されるように生産性の向上策として『コスト削減=リストラ策』がもて囃されたが、革新的技術への投資で生産性は向上する事をデミング博士は述べられている。
平成時代の品質軽視はデミング博士の教えと真逆の事が広く社会を覆い、停滞した時代であったが、1995年前後からインターネット技術が普及し始め、情報の再生産性は著しく向上した時代でもあった。
現在、ブロックチェーン技術と密接に関係しあうIoT技術及びその膨大なデータ解析にAI(人工知能)が適用され始め、プロセスイノベーションが世界規模で展開されている。
この三大技術の組合せによる普及の推移を想像してみよう。
新技術の普及を考える場合には、普及率D(t)は0%より大きく100%より小さいと考えられる(0<D(t)<1) 。
普及の上限はK=1である。
$$以上の前提でロジスティックス曲線型の普及を検討する。( N_{0} をD_{0}に置き換える)$$
\begin{aligned}D(t)=\dfrac {K}{1+Ae^{-rt}}=\dfrac {K}{1+\dfrac { K -D_{0}}{D_{0}}e^{-rt}}\\ \end{aligned}
$$ 普及率の初期値 D_{0} を D_{0}= 0.01 $$
と仮定する。
$$A=\exp \left( -c\right) =\dfrac {K-D_{0}}{D_{0}}=\dfrac {1-0.01}{0.01}=99$$
である。また、r=0.25と仮定すると
$$ D\left( t\right) =\dfrac {1}{1+99\cdot \exp \left( -0.25\cdot t\right) } $$
となる。t=0からt=40までの区間について、この式のグラフを描く
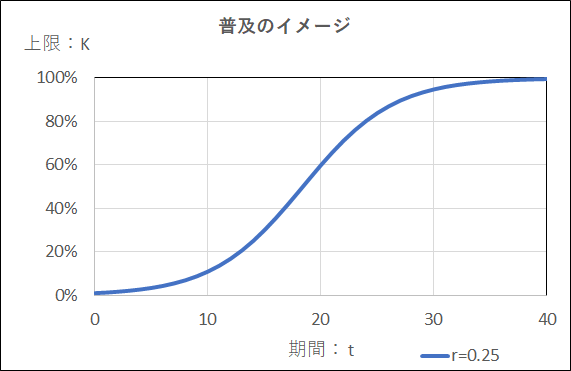
期間tの単位を半年、四半期等で評価しても良い。

農作物の生育過程をロジスティックス曲線にて分析した事例として以下を紹介する。
ロードセルを利用した温室メロン生育の観察~静岡県農業水産部 研究調整室(平成15年2月発行 あたらしい農業技術 No.389)
https://www.agri-exp.pref.shizuoka.jp/newtech/pdf/389_H14.pdf
ロジスティックス曲線 による生育予測が有効である事が確認できる。
■■ロジスティックス曲線とその微分:AIへの応用■■
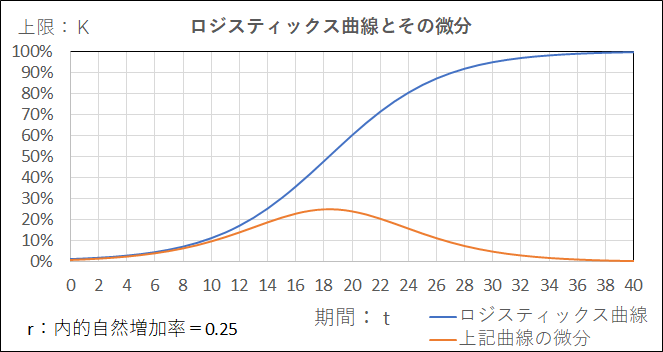
AI(人工知能)テクノロジーで話題になっているニューラルネットワークの2値分類問題(予測)にシグモイド関数(ロジスティックス曲線を含む)の微分が利用されている。
微分する事によりAI(人工知能)テクノロジーによる『生育AI診断システム』として展開させる事も可能になり、必要なデータ入手もIoT等を活用する事で統合化できる。