出典:https://www.youtube.com/watch?v=eIeeFVaAxaM&t=3568s&ab_channel=rikenchannel








■確率勾配降下学習法(甘利)
⇒1967年代に発表
⇒冬の時代に人工知能を研究(紙と鉛筆で)
・1986年にジェフリー・ヒントン教授らが再発見
(2024年ノーベル物理学賞を受賞)

■人工知能の理論と実験の交流を組織化
⇒伊藤正男


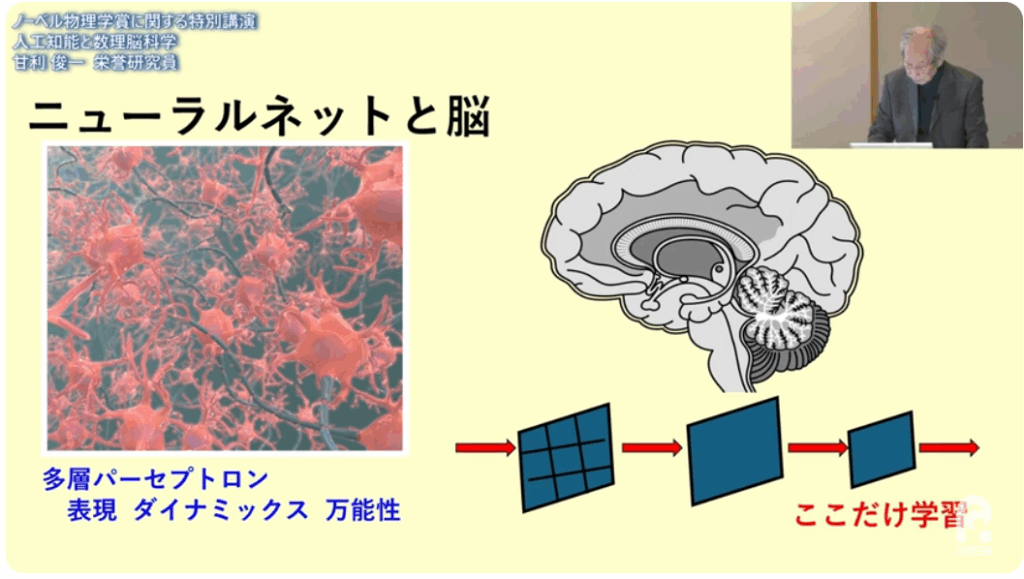
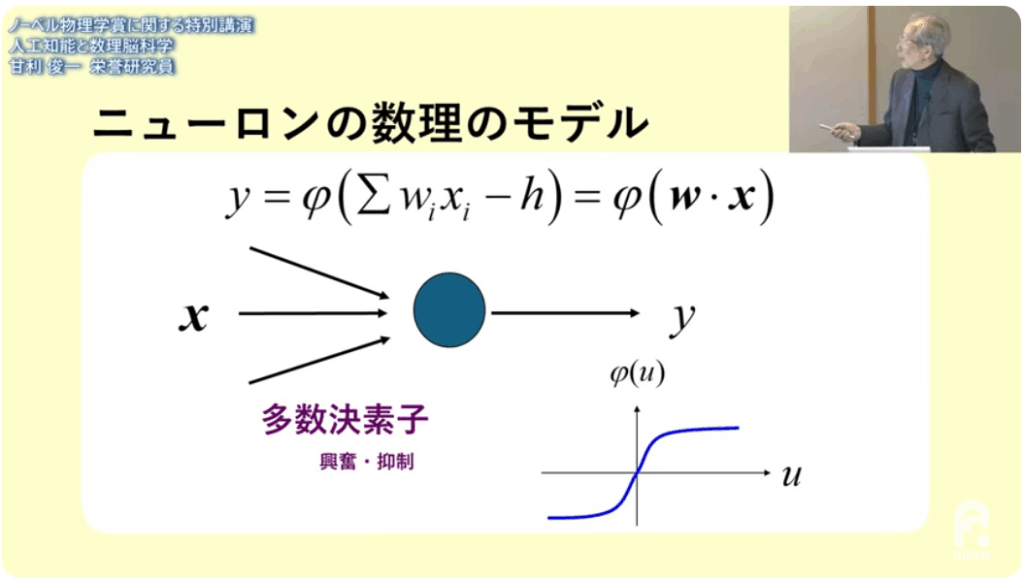
■重み付けによる線形関数計算
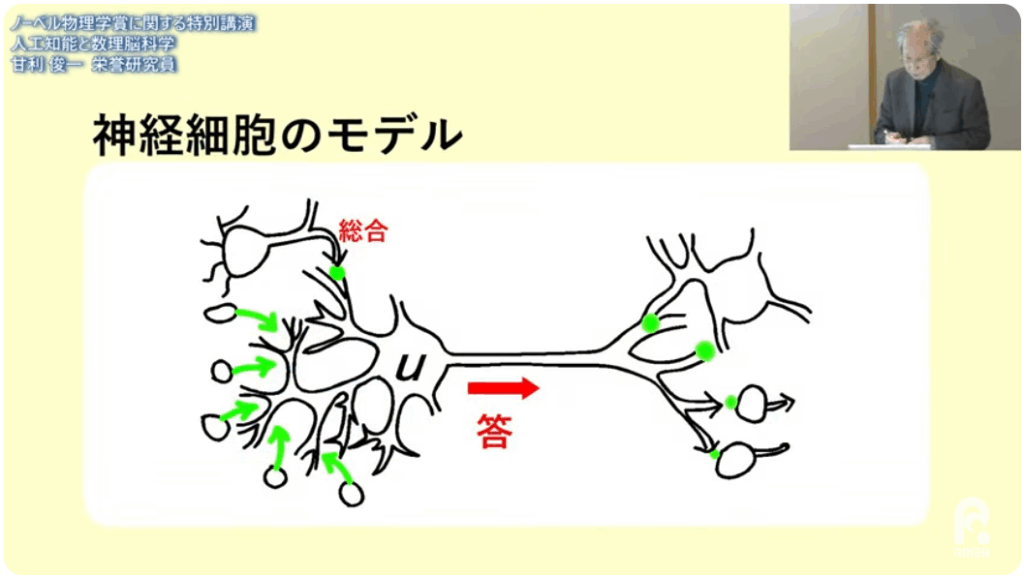
■計算モデル
⇒シグモイド関数
■ニューロンを多数にしたモデル
⇒多層パーセプトロン
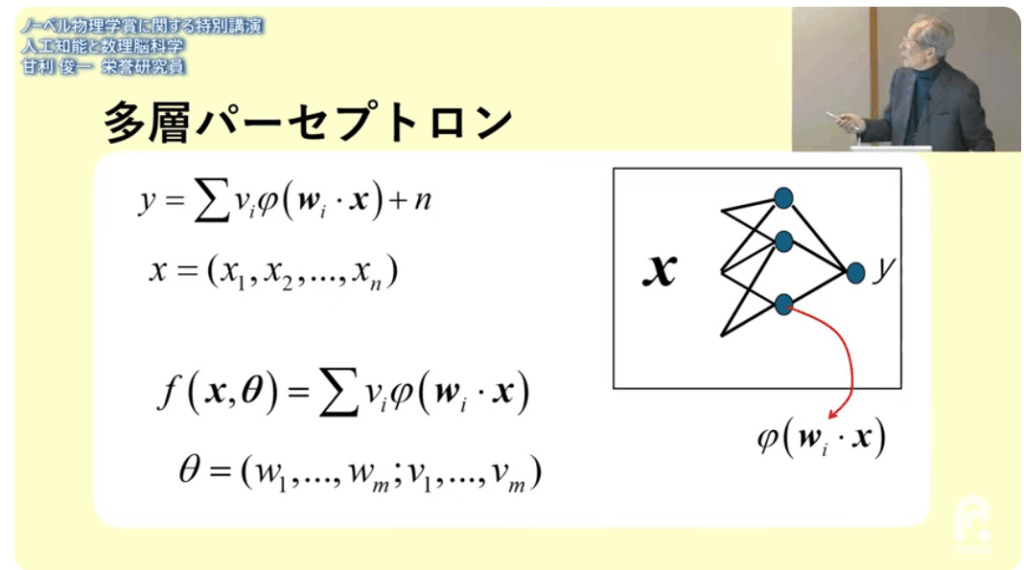

■近似精度の向上
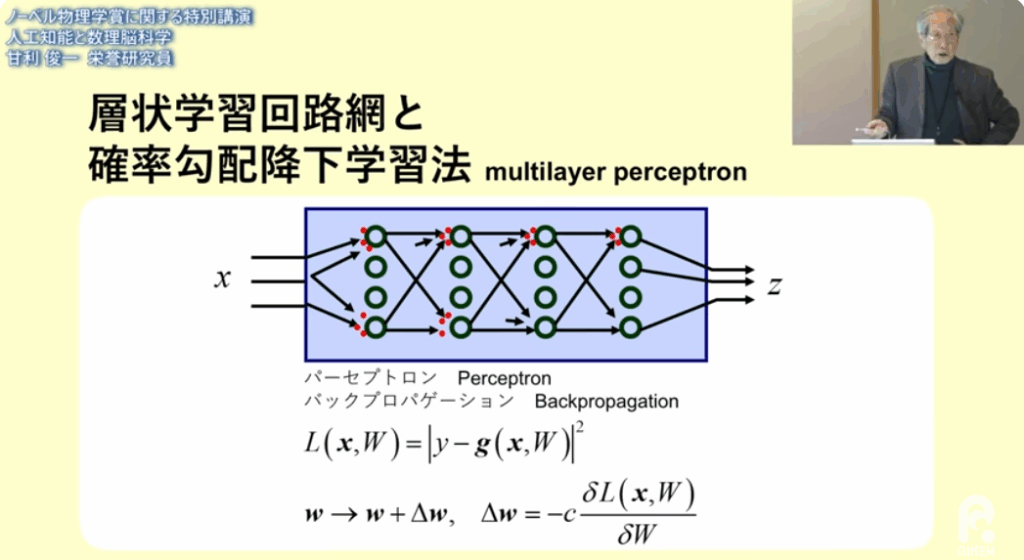
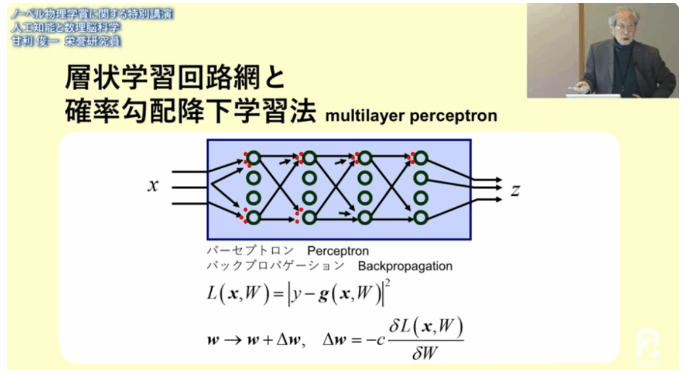
・層状学習回路網
・確率勾配降下学習法
⇒答え=Zが違えば
⇒最後の層(学習できる層)のパラメータを少し変えれば良い
(+に少し変えるか-に少し変えるだけで良い)
⇒誤差をパラメータで偏微分する
⇒偏微分の事を勾配
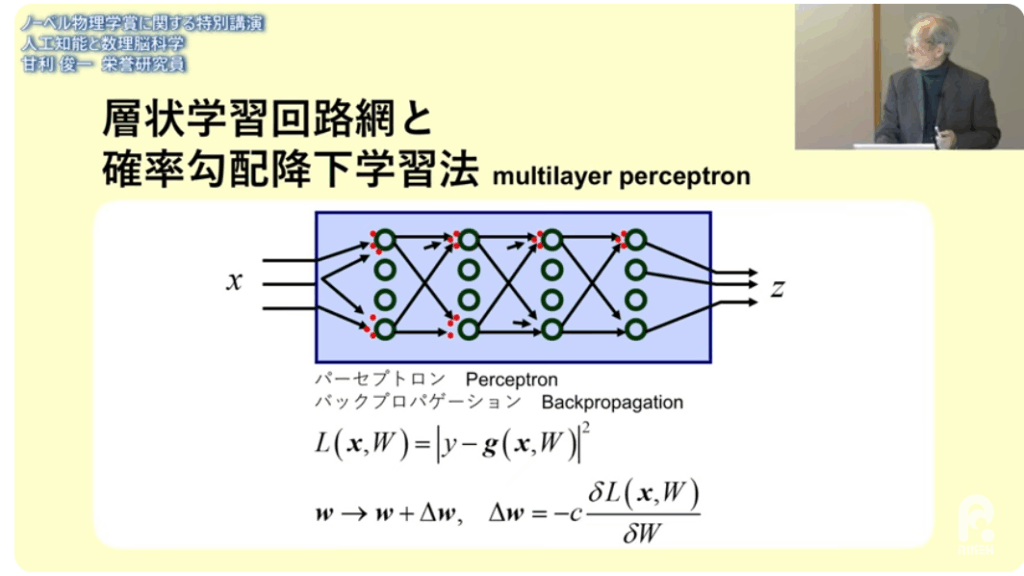

■中間層の重み付け(パラメータ)の変更をどうするか?
・中間層の学習をどうしたら出来るか
⇒0,1を取る2値の論理素子を使った
⇒重みwを少し変えるというシナリオが成り立たない
■アナログニューロンを使えば
・中間層の学習ができる
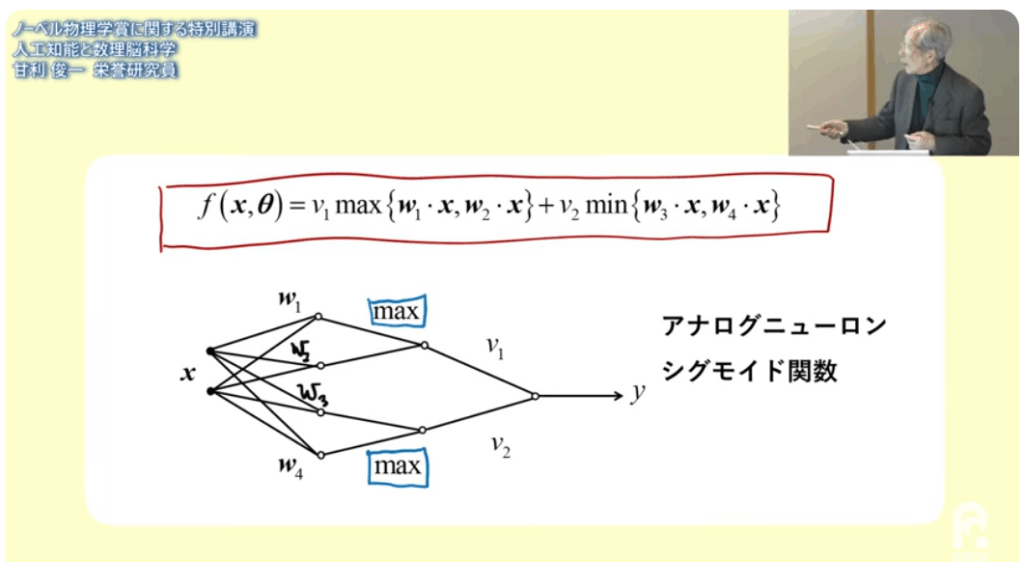
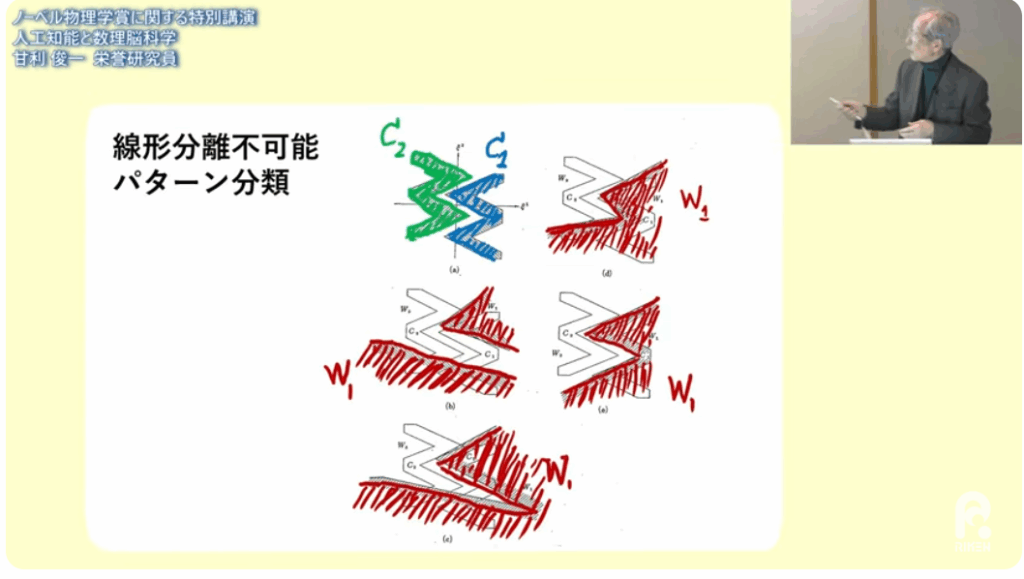
■線形分離
・分離ができなければパーセプトロンが働かない
・アナログニューロンなら
⇒勾配降下法で学習できる
⇒世界初の多層学習シュミレーションを開発した
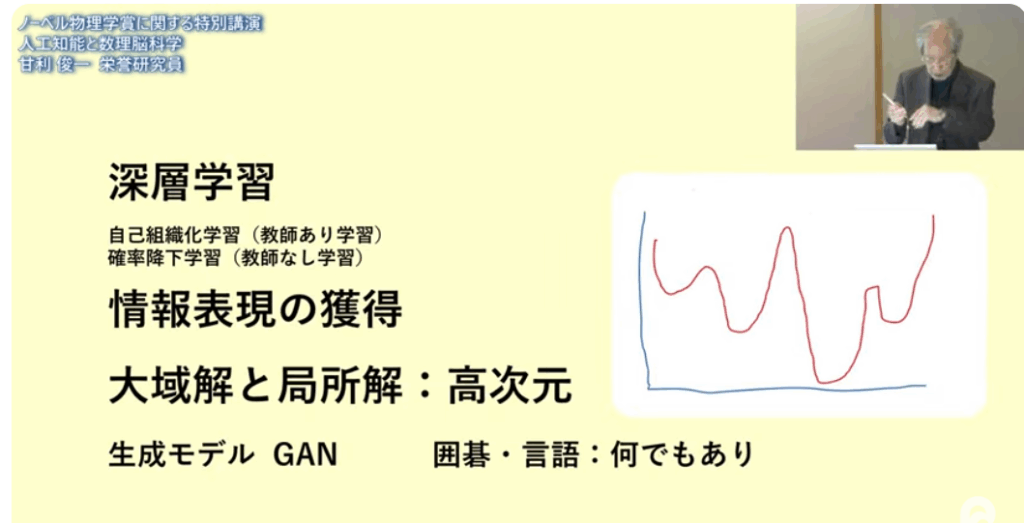
■多層学習が何故良いと思わなかったか
・パラメータを変えると
⇒誤差が大きくなる(右下図)
⇒誤差が一番小さくなる初期値を見つけるのは至難である
⇒だからダメであると思った
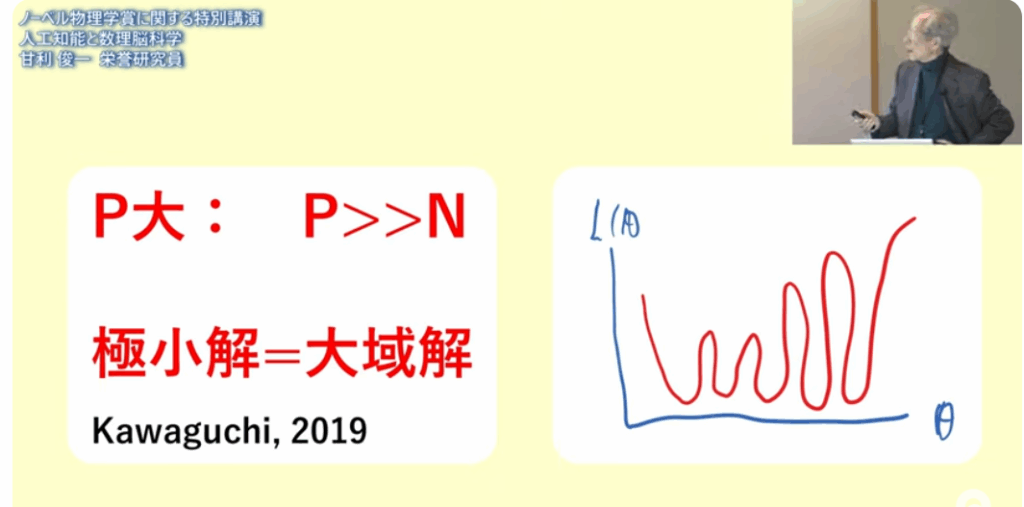
■ところが深層学習を大規模なパラメータでやってみると
・ローカルミニマムが途中で引っ掛かることはない
⇒パラメータを増やせば、皆、底まで行く
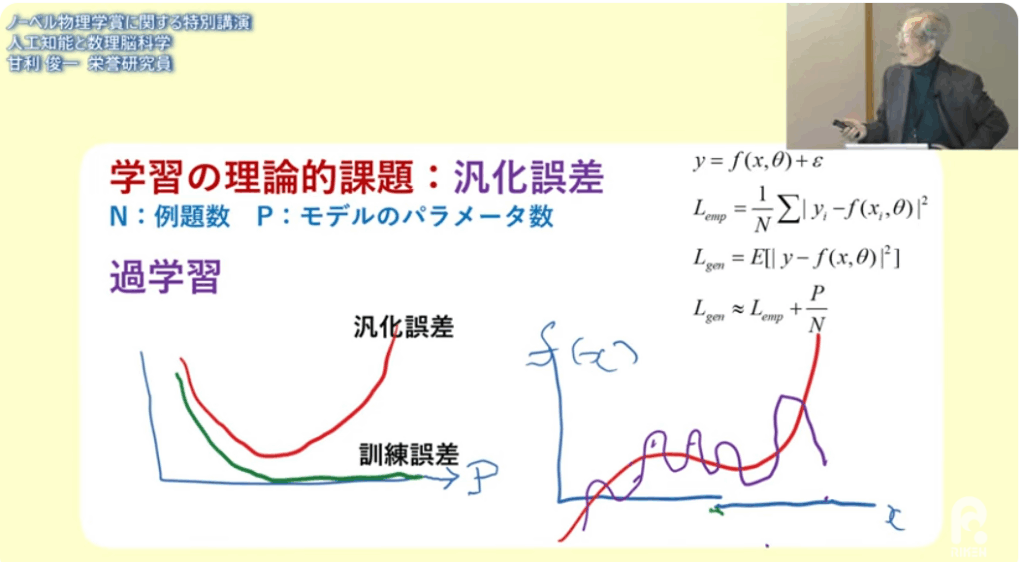
■過学習の問題
・例題の数よりパラメータを多くすると
⇒何でもありになる
⇒統計学の観点から例題は誤差を含んでいるので良くない
・誤差を少なくするためには
⇒例題の数よりもパラメータを少なくする必要がある
■誤差の最小化は偏微分で行う
■深層学習でパラメータを大規模化すると
・結果オーライで何故か上手くいった
⇒2024年でもまだその理由が良く分かっていない
⇒理論家が頑張らなきゃいけない
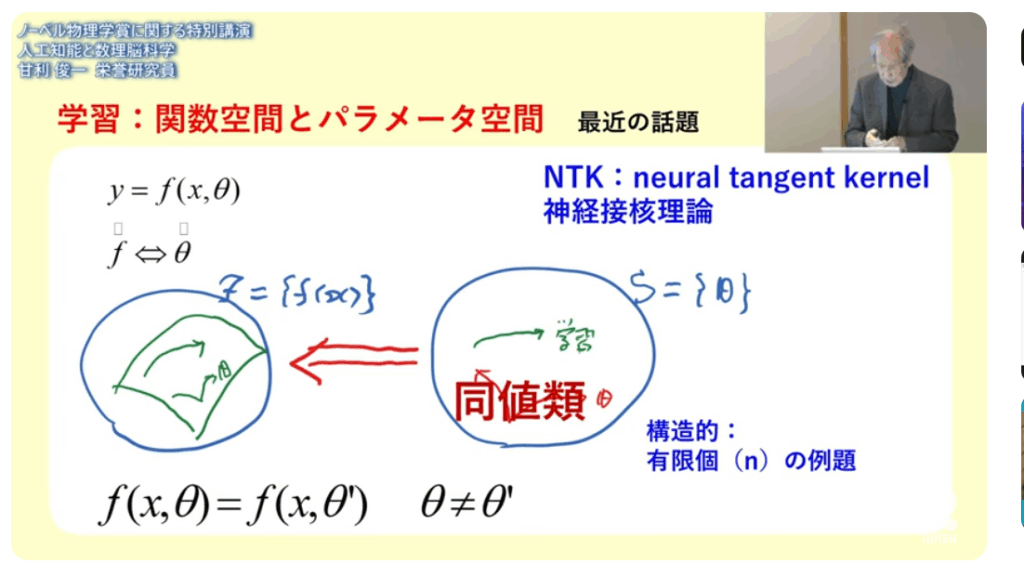
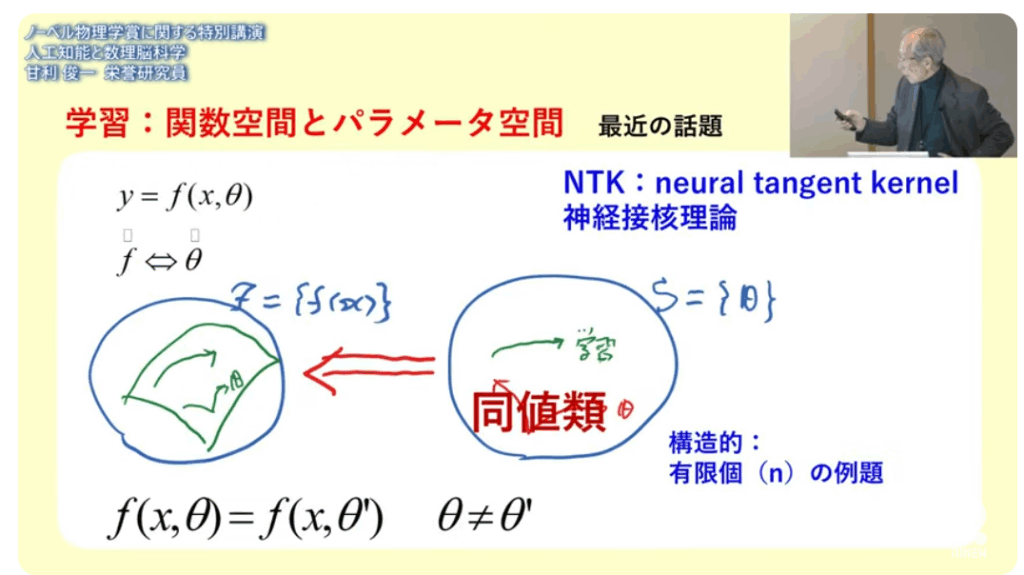
■NTK(neural tangent kernel)
・ある確率に基づいてランダムに初期値を選びなさい
⇒例えば正規分布からそれぞれ独立にえらびなさい
⇒学習させると正解はランダムの極近くにある
⇒これは妙である(ランダムなら何処でも取れる)
⇒正解が至る所にバラバラにある
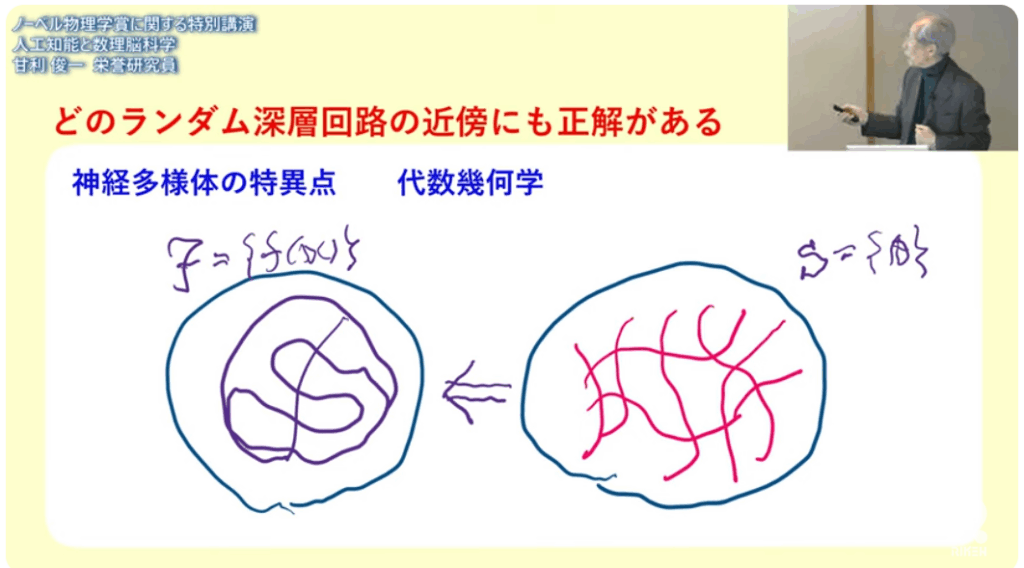
■神経回路には特異点がある
■パラメータが違っていても(θ)とθ’)
⇒それが実現する関数は
⇒同じに(同値)なってしまうのだ
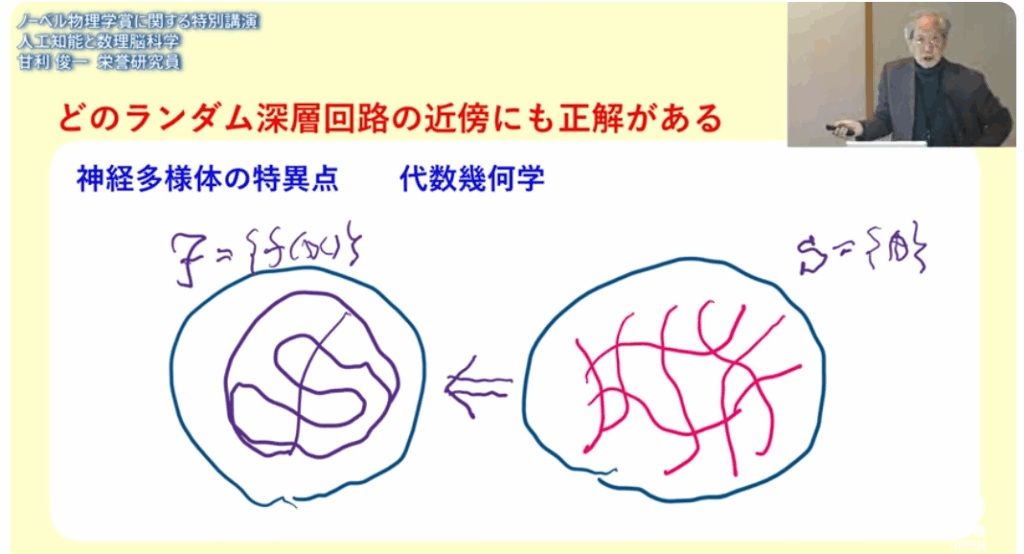
⇒複雑怪奇な事が起きる
■任意のランダム回路の近傍に正解がある
・統計推論より






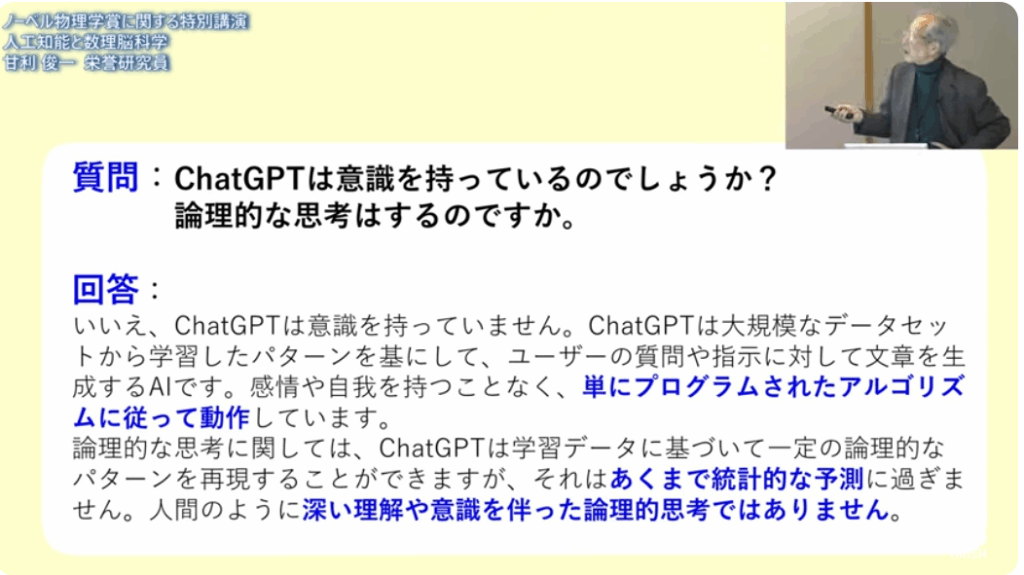





■理論が先導してダウン・サイジングをしなくてはならない
・現在は大量・大規模化で進んでおり、出力(答え)を導く理論は不明

■人間の脳は
・多数のニューロンの共同作業で次から次へと進む並列処理
⇒1ステップ毎にプログラムされて進む直列処理
⇒それでも上手く動く